Liquid Chromatography Column Design and Dimensional Analysis of the van Deemter Equation

The fundamental mechanisms of band broadening are usually introduced to students through the van Deemter equation. Dimensional analysis of this equation can give physical meaning to the equation coefficients and enhance our understanding relative to qualitative descriptions. This approach can also guide improvements to future liquid chromatography (LC) column designs.

Think back to when you first learned about the van Deemter equation:

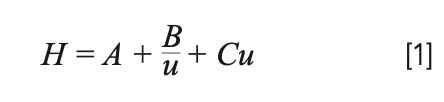
If it was anything like our experience, it was in your first lecture about column chromatography. We learned about the three terms of the equation (A, B, and C) that represent the three “uncoupled” mechanisms contributing to the somewhat abstract concept of band broadening and how they related to the mobile phase velocity (u). These terms were paired with three simple cartoons to describe the movement of molecules through a packed bed (Figure 1). This description worked well, at least for passing the exam on chromatography and explaining observations for our course laboratory notebooks. It wasn’t until we began our research projects on the packed bed microstructures of capillary liquid chromatography (LC) columns (1) that we started to think about the units of these terms. It confused us as to why dimensional analysis of the van Deemter equation isn’t highlighted more widely. The equation gives plate height, H, with units of length. As the terms of the equation are only modified by velocity, unit analysis is straightforward. Here, we hope to convince you that this approach to the van Deemter equation is equally as important as the cartoons (or metaphors (2)) and a conduit to describing the fundamental mechanisms that will direct the future of column design.

FIGURE 1: Representative cartoon representation of van Deemter term-based description of band broadening commonly used in introductory analytical chemistry courses.

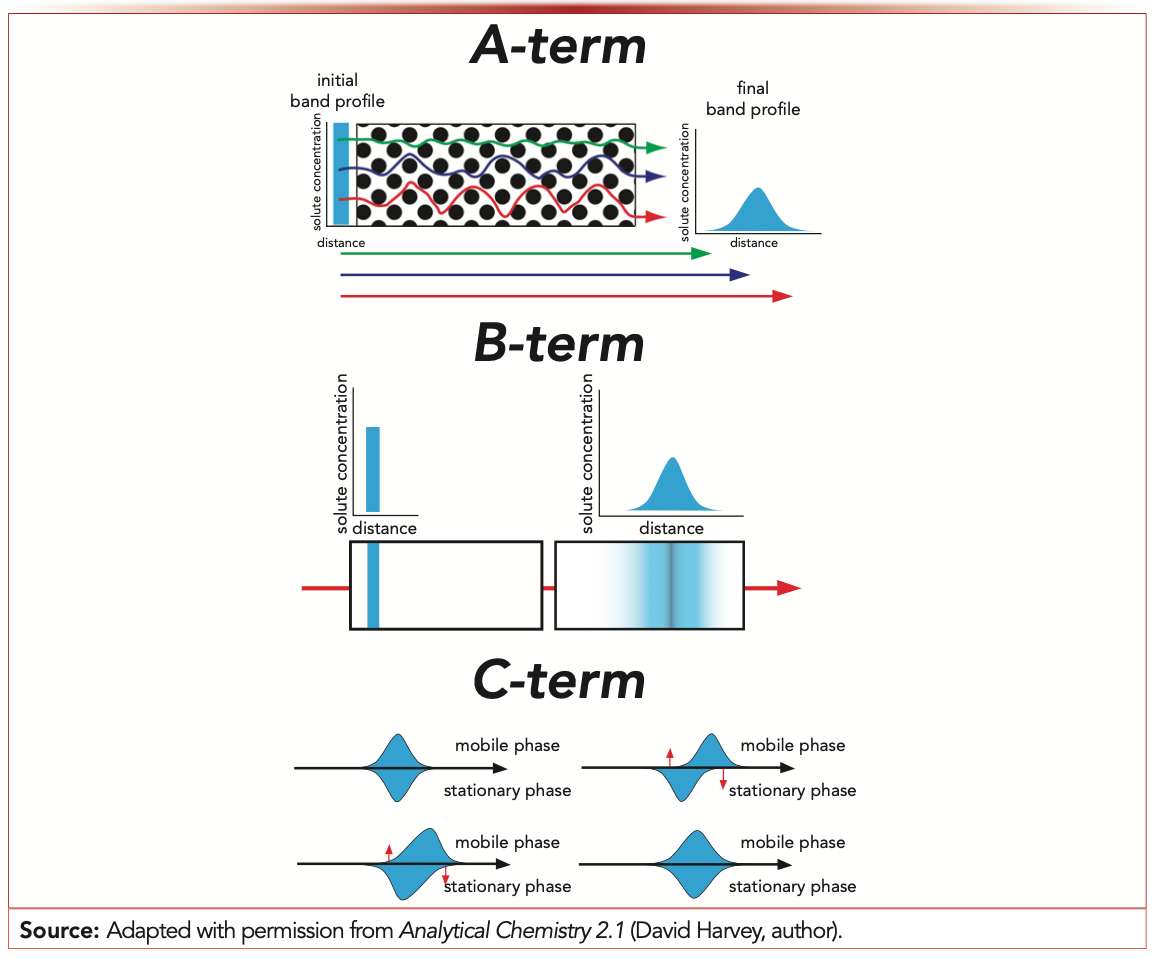
The A-term, related to multiple flow paths, has length units (cm, or more realistically, μm) as it matches the length units of H. Although deeper theory on band broadening often separates this “eddy diffusion” term into various components based on the scale over which the flow path differences are being compared (3), the simplest way to connect modern LC to this term is through the idea of flow path homogeneity. Effectively, the more “perfectly ordered” a column structure is, the fewer different flow paths (inherently of different lengths) that a single molecule can transverse. An open-tubular LC column (4) best demonstrates this because in an open-tubular LC column, there is essentially one primary flow path through the column that can be extended to multichannel capillaries, where a number of parallel flow paths are found within a single capillary (5). In these systems, small variations in diameter (a length term!) between parallel channels can increase bandwidth. To better replicate a chromatographic “bed,” the ordered structures (for example, pillar arrays) can be generated through microfabrication (6) or three-dimensional (3D) printing (7,8). In these systems, a much larger surface area is available compared to open-tubular formats to increase the loading ability. However, based on the optimized designs, multiple flow path broadening is still lower than what may be observed in a less ordered packed bed or monolith (6). We imagine further reduction of this term will continue to be a focus of the future of column chromatography. A potential approach that allows for the surface area advantages of particles but ensures ordered structures is the patterned layering of particles (9). Similar in the way the term is eliminated in capillary electrophoresis (CE), mitigation of the drawbacks of column sample loading through the implementation of more-sensitive detectors will surely be a goal in the future of column design.

The B-term, which represents longitudinal diffusion, has units that are used to describe diffusion coefficients (cm²/s). This term is usually met with some understanding when first introduced because the concepts of molecular diffusion apply broadly within the world of chemistry. Longitudinal diffusion occurs inherently throughout the separation process, even when flow is stopped, or analytes are so highly retained that they are effectively “stuck” on the column. A primary focus of fundamental LC research in recent years has been the measurement of various contributions to the overall diffusional broadening that occurs as analyte molecules move through a column (10). Dimensional analysis of the B-term suggests the spatial contribution to H can be reduced by limiting the time over which diffusion is allowed. In practice, it leads to an increase in the mobile phase velocity. It is rare that someone chooses to develop a slow LC method where broadening dominates because of longitudinal diffusion. Instead, we must think about modern applications where this process may be the most relevant. Recently, both step (11) and reverse (“negative”) (12) gradients have been proposed to help significantly increase the resolution between closely eluted peaks in monoclonal antibody samples, even pushing values to “infinite” resolution. This application is feasible because the “S-term” relating retention and eluent strength is incredibly steep for large molecules and because the diffusion coefficient of large molecules is already low (13). As these techniques are only effective on large molecules with very small diffusion coefficients, B-term broadening is not a primary concern even in specific instances of long separations (especially when additional peak focusing effects are considered). Because diffusion can never be eliminated, the true focus with continued progress in LC development related to this term is rather how to design separations in which its contribution plays a minimal role in bandwidth. Fortunately, most of the broadening because of this term is eliminated if we simply speed up separations.

The C-term, resistance to mass transfer, is calculated in time units. At the introductory level, it is attributed to the series of steps, each with a finite time, that an analyte molecule undergoes to partition across the column’s stationary and mobile phases. The slower this process, the more band broadening occurs, and it is especially detrimental at high mobile-phase velocities. A number of recent advances to limit this broadening have enabled efficient separations of small molecules at high speeds (14), with the focus now shifting to tackle analytical challenges associated with modern therapeutics that largely consist of biomolecules. As these large biomolecules have low diffusion coefficients, they are at odds with rapid mass transfer and thus, low C-term values. The future of chromatographic beds and separation supports for biomolecules will focus on facilitating efficient access to the stationary phase surface. Limiting the distance that these larger molecules need to travel (by using smaller particles) or by reducing the distance that molecules have to travel once they enter a pore (with core-shell morphologies, especially those with ordered pore structure (15)) will be critical. Some wide-pore superficially porous particles (SPPs) already have shown utility this way (16,17). To fully access the stationary phase area of a particle, the pore diameter should be large enough to ensure unrestricted access to the pore volume by the largest molecules in a mixture. Different selectivity for large molecules can be observed when similar stationary phases that primarily differ in pore diameter are used (18). Although many of these variations have been considered and developed for particle-packed columns, thinking about expanded stationary phase area on some of the other column types described to have lower A-term effects may help increase the rate of their adoption. Again, we think implementation of open tubes or nonporous stationary phase supports will grow as detection capabilities improve. To truly achieve diffusion-limited broadening, eliminating stationary phase effects (and the lengths and times associated with them) is necessary. When analytes are amenable to these types of separations (for example, CE and ion mobility spectrometry), peak widths are far narrower and time scales are notably shorter than what can typically be achieved in a packed column chromatographic separation (19,20). The increase of these techniques in prevalence and their coupling to mass spectrometry (MS) for analyzing complex systems implies that these will also be powerful tools in the future of chemical separations, when applicable to a given sample.

Whether it is the length units of the A-term, diffusion coefficients of the B-term, or time scales of the C-term, dimensional analysis provides and important way of describing the van Deemter equation, supplementing introductory cartoons and providing an avenue to exciting advances in chromatographic research. These fundamental principles will continue to drive the field as the chromatography community continues to strive for ever more efficient separations!

References

(1) L.E. Blue, E.G. Franklin, J.M. Godinho, J.P. Grinias, K.M. Grinias, D.B. Lunn, and S.M. Moore, J. Chromatogr. A 1523, 17–39 (2017). https://doi.org/10.1016/j.chroma.2017.05.039.

(2) Crawford Scientific Blog, Van Deemter Equation – The Lockdown Guide. https://www.crawfordscientific.com/chromatography-blog/post/van-deemter-equation-the-lockdown-guide (accessed July 2022).

(3) J.C. Giddings, Dynamics of Chromatography, Part 1: Principles and Theory (Marcel Dekker, New York, 1965).

(4) S.C. Lam, E. Sanz Rodriguez, P.R. Haddad, and B. Paull, Analyst 144, 3464–3482 (2019). https://doi.org/10.1039/c9an00329k.

(5) S. Currivan, N. Upadhyay, and B. Paull, TrAC – Trends Anal. Chem. 102, 322–331 (2018). https://doi.org/10.1016/j.trac.2018.03.008.

(6) G. Rozing, Microchem. J. 170, 106629 (2021). https://doi.org/10.1016/j.microc.2021.106629.

(7) C. Salmean and S. Dimartino, Chromatographia 82, 443–463 (2019). https://doi.org/10.1007/s10337-018-3671-5.

(8) F. Matheuse, K. Vanmol, J. Van Erps, W. De Malsche, H. Ottevaere, and G. Desmet, J. Chromatogr. A 1663, 462763 (2022). https://doi.org/10.1016/j.chroma.2021.462763.

(9) S. Verloy, B. Vankeerberghen, I.S.M. Jimidar, H. Gardeniers, and G. Desmet, Langmuir 38(25), 7709–7719 (2022). https://doi.org/10.1021/acs.langmuir.2c00593.

(10) G. Desmet, K. Broeckhoven, S. Deridder, and D. Cabooter, Anal. Chim. Acta 1214, 339955 (2022). https://doi.org/10.1016/j.aca.2022.339955.

(11) S. Fekete, A. Beck, J.L. Veuthey, and D. Guillarme, Anal. Chem. 91, 12954–12961 (2019). https://doi.org/10.1021/acs.analchem.9b03005.

(12) S. Fekete, A. Murisier, J.M. Nguyen, M.A. Lauber, and D. Guillarme, J. Chromatogr. A 1635, 461743 (2021). https://doi.org/10.1016/j.chroma.2020.461743.

(13) L.R. Snyder, J.J. Kirkland, and J.W. Dolan, Introduction to Modern Liquid Chromatography (John Wiley & Sons, Inc., Hoboken, 3rd ed., 2010). https://doi.org/10.1002/9780470508183.

(14) A.S. Kaplitz, G.A. Kresge, B. Selover, L. Horvat, E.G. Franklin, J.M. Godinho, K.M. Grinias, S.W. Foster, J.J. Davis, and J.P. Grinias, Anal. Chem. 92, 67–84 (2020). https://doi.org/10.1021/acs.analchem.9b04713.

(15) T.-C. Wei, A. Mack, W. Chen, J. Liu, M. Dittmann, X. Wang, and W.E. Barber, J. Chromatogr. A 1440, 55–65 (2016). https://doi.org/10.1016/j.chroma.2016.02.018.

(16) B. Wei, B. Zhang, B. Boyes, and Y.T. Zhang, J. Chromatogr. A 1526, 104–111 (2017). https://doi.org/10.1016/j.chroma.2017.10.040.

(17) B.M. Wagner, S.A. Schuster, B.E. Boyes, T.J. Shields, W.L. Miles, M.J. Haynes, et al, J. Chromatogr. A 1489, 75–85 (2017). https://doi.org/10.1016/j.chroma.2017.01.082.

(18) J.M. Godinho, J.A. Naese, A.E. Toler, B.E. Boyes, R.A. Henry, J.J. DeStefano, and J.P. Grinias, J. Chromatogr. A 1634, 461678 (2020). https://doi.org/10.1016/j.chroma.2020.461678.

(19) N.G. Batz, J.S. Mellors, J.P. Alarie, and J.M. Ramsey, Anal. Chem. 86, 3493–3500 (2014). https://doi.org/10.1021/ac404106u.

(20) G.F. Verbeck, B.T. Ruotolo, K.J. Gillig, and D.H. Russel, J. Am. Soc. Mass Spectrom. 15, 1320–1324 (2004). https://doi.org/10.1016/j.jasms.2004.06.005.

James P. Grinias is an Associate Professor of Chemistry at Rowan University, in Glassboro, New Jersey. Direct correspondence to: grinias@rowan.edu

Justin M. Godinho is with GlaxoSmithKline.