Perspectives on the Use of Retention Modeling to Streamline 2D-LC Method Development: Current State and Future Prospects
The history of multidimensional liquid chromatography (MDLC) has been dominated by methods that have been developed using highly empirical, experience-driven, trial-and-error approaches. These approaches have been sufficient in progressing the field forward scientifically, primarily in academic research laboratories. However, more widespread usage of multidimensional separations will require more systematic approaches to method development that rely less on user experience and lower the barriers to development and use of methods by a wider community of users. In this mini-review, we discuss recent research aimed at developing such systematic, model-driven approaches to streamline method development and speculate about likely advances in the same direction in the near future. It seems likely that such model-driven approaches would be particularly helpful for methods developed for analyzing biopharmaceutical molecules, which tend to be very sensitive to slight changes in method conditions (for example, mobile phase composition).
In the late 1980s, the introduction of DryLab software by Snyder, Dolan, and co-workers changed the way researchers approached method development for one-dimensional liquid chromatography (1D-LC) (1,2). This work made it clear that method development could be approached in a more systematic way than how it was done in the past. The idea was to use software to calculate the expected resolution for many hypothetical experiments involving different variations in parameters affecting elution, such as mobile phase composition, temperature, and gradient time. Using retention data from a few experimental “scouting runs” to build a retention model, Snyder and Dolan demonstrated that the resulting models were accurate enough to predict the conditions that should be tried in search of an optimal set of method conditions. Since this time, the DryLab software has become more sophisticated, and other software packages with similar capabilities have been introduced by other commercial vendors.
It is well recognized in the multi-dimensional separations community that several challenges associated with method development for two-dimensional LC (2D-LC) continue to hamper wider use of the technique. Currently, 2D-LC method development relies heavily on user experience and trial-and-error approaches. In spite of the tremendous success of DryLab and related software packages in facilitating method development for 1D-LC, similar concepts have only been applied to 2D-LC method development workflows recently. In this mini-review, we briefly summarize these efforts for both non-comprehensive and comprehensive 2D-LC methods, and speculate on likely future developments in this area.
Retention Modeling for Non-Comprehensive 2D-LC Methods
In a pair of papers from 2014 and 2016, Andrighetto and others began discussing the potential of using retention modeling during development of 2D-LC methods for forensic science applications (3,4). The first of these papers focused on a heartcut 2D-LC method aimed at using the second dimension (2D) for resolution of ephedrine and pseudoephedrine, which are generally difficult to separate by reversed-phase (RP) LC. The second paper showed results obtained for an experimental comprehensive 2D-LC separation of illicit amphetamines obtained after predicting optimal first and second dimension separations using the DryLab software. This work showed the utility of retention modeling software for reducing the amount of experimental work needed to develop a method. However, it is clear from the resulting chromatograms that the predictions were not as accurate as one would like for routine method development, leaving room for improvement of the approach.
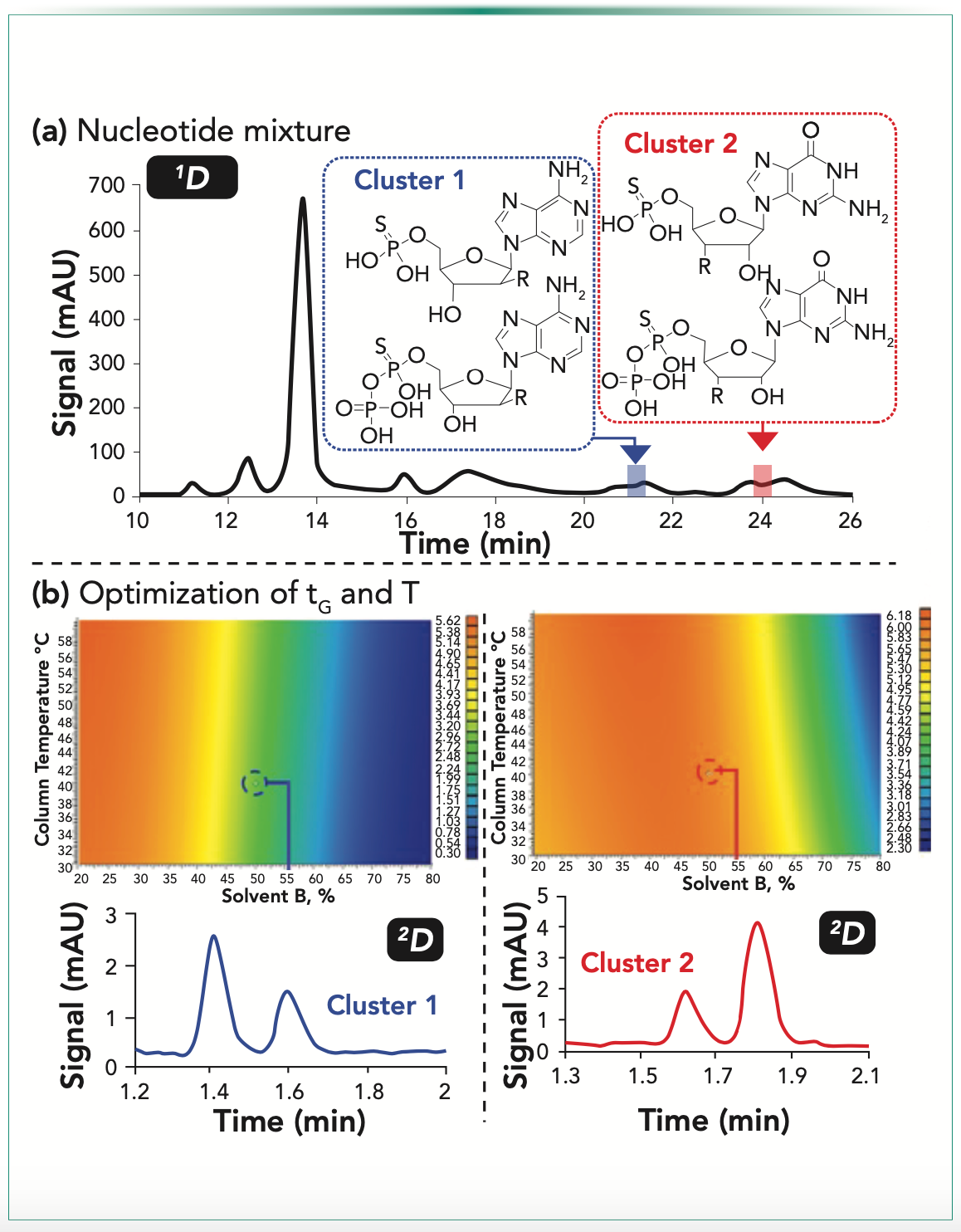
More recently, Regalado and co-workers have been working toward using retention modeling to streamline development of non-comprehensive 2D-LC methods for pharmaceutical analysis. In the first of two papers focused on development of LC-LC methods, Makey and others showed the value of building retention models for 2D chiral separations to streamline the process of finding elution conditions that could resolve compounds not separated by an achiral first dimension (1D) separation (5). These models yield resolution maps that show the dependence of resolution on variables, such as temperature, gradient time, or mobile phase composition, for a pair of analytes not separated by the 1D column. These maps then enabled the quick identification of optimal conditions for a rapid resolution of the pair in the second dimension. Whereas the retention models in this work were built using retention data from 1D-LC experiments, a second paper from Haidar Ahmad and others showed that the data needed to build the retention models can be obtained from 2D-LC separations themselves, using a series of methods where the elution conditions used in the second dimension are changed (temperature, gradient time) while holding the other parameters constant (6). This approach helps account for some effects that are difficult to model for when the scouting runs used to build the model are based on 1D-LC separations, such as mobile phase mismatch and the injection of large volumes of 1D mobile phase into the 2D column. An example outcome of this approach is shown in Figure 1, where the resolution maps for two pairs of compounds that overlap in the first dimension are shown, along with the experimental 2D separations that show the predictive value of the retention models.
FIGURE 1: (a,b) Development of an LC-LC method for separation of a nucleoside mixture using ion-exchange separations in both dimensions. Adapted with permission from I.A. Haidar Ahmad, D.M. Makey, H. Wang, V. Shchurik, A.N. Singh, D.R. Stoll, I. Mangion, and E.L. Regalado, In Silico Multifactorial Modeling for Streamlined Development and Optimization of Two-Dimensional Liquid Chromatography, Anal. Chem. (2021). https://doi.org/10.1021/acs.analchem.1c01970. Copyright 2021 American Chemical Society.
Retention Modeling for Comprehensive 2D-LC Methods
The prospect of simplifying method development through simulation of separations and retention modeling is perhaps even more attractive for comprehensive 2D-LC. In this case, all 1D effluent fractions are subjected to a 2D separation. Innovations in modulation technology have improved the ease of coupling different separation types, but they have also increased the number of variables that must be optimized. For 2D-LC, variables affecting elution and performance in the two dimensions are highly interdependent, including those related to injection, modulation, and detection (7).
Motivated by this opportunity, the scouting gradient-based approaches developed for 1D-LC have also been developed for 2D-LC, like in the program for interpretive optimization (8,9). This tool relied on data obtained from scouting 2D-LC experiments to construct retention models for both dimensions, and then a large number of hypothetical chromatograms were simulated. The Pareto optimality principle was applied to assess the quality of the simulated separations by computation of chromatographic response functions and descriptors, such as resolution and analysis time. Muller and others later published methods for the kinetic optimization of 2D-LC separations involving hydrophilic-interaction chromatography (HILIC) and RP separations (10). In their work, the authors considered not only gradient elution programs but also kinetic parameters including column length and temperature.
Although the initial development of these tools demonstrated proof-of-concept for software-assisted method optimization in 2D-LC, practical implementation is not straightforward yet because of a number of bottlenecks. For example, accurate retention modeling of the 1D separation is difficult because of the limited sampling of the 1D effluent. A reduction in the number of data points available to describe the shapes of 1D peaks complicates computation of the first moment (that is, the retention time [tR]). Conversely, although there is a surplus of data points in the second dimension, the actual peak shape may be affected by mobile phase mismatch and modulation processes (11). Such factors may significantly affect the obtained tR and thus directly impact the robustness of the retention model.
Therefore, it is important that the 2D peak shapes are accurately simulated. The groups of Stoll and Rutan addressed these issues in a series of papers (12,13) in which the actual peak elution profile is calculated as the analyte band progresses through the column. Peak dispersion is also relevant for the computation of the chromatographic response function that drives the optimization process, which was also observed by Pirok and others who used a basic van Deemter model to simulate peak broadening (8). Although minimal tR prediction errors were observed for a strong anion-exchange (SAX)×ion-pair (IP)-RP separation, the authors were not able to accurately account for the dispersion, and thus, the resolution computed for the separation was inaccurate. Tyteca and Desmet recently investigated chromatographic response functions (14) and their effects on retention modeling-based method optimization (15).
The scouting gradients used to obtain the experimental data needed to train simulations for 2D-LC also present a bottleneck. Like in 1D-LC separations, the retention models are most accurate when predicting separations for conditions that resemble those used for the scouting experiments (16). Consequently, the choice of specific conditions for the scouting methods may bias the optimization process. For polymer separations, pump-induced gradient deformations may be a bigger threat. Given that small deviations in the organic modifier concentration can result in the sudden elution of a polymer, an inaccurate description of the effective solvent gradient program may significantly distort the retention model (17).
Finally, it is important to note that comprehensive 2D-LC is primarily used for analyzing highly complex samples. The number of analytes to track during method development is thus large, and it can be tedious to manually find them in chromatograms where elution conditions have been changed for the purpose of constructing retention models. Peak tracking algorithms that can automatically track peaks in complex chromatograms and extract their retention times from raw chromatograms are thus essential; although the utility of such algorithms has been demonstrated, they still require improvement before they can be implemented routinely (18).
With the increasing popularity of shifting gradient programs used in RP×RP separations (19) and the challenges described above, the need for software tools to help optimize such separations is only growing. One interesting approach that may be up to this challenge is the use of Bayesian optimization. Unlike neural networks and related tools, Bayesian optimization is a machine learning tool that is well suited to low-data applications. It exploits Bayes’ theorem to include and evaluate prior separation data for computation of posterior Pareto optimal methods. The technique was recently investigated in combination with retention modeling in a computational study (20). Because it relies solely on chromatographic response functions to drive the optimization process, the approach does not require peak tracking methods.
Ultimately, it is likely that advanced machine learning tools will play an important role in future method optimization strategies for 2D-LC, but it also seems likely that the knowledge provided by retention modeling can decrease the computational cost of such machine learning processes.
Summary
The 2D-LC separations field seems poised to benefit tremendously from the more extensive use of software-assisted method development. Proof-of-concept studies for both non-comprehensive and comprehensive 2D-LC separations have demonstrated that retention modeling can reduce the amount of trial-and-error needed to develop effective methods. Although most work in this area to date has largely focused on separations of “small molecules,” our expectation is that model-driven method development should be more valuable for methods focused on analyzing larger molecules, such as peptide and protein therapeutics. The retention of these and other large molecules tend to be highly dependent on separation conditions (for example, mobile phase composition), and the ability to reliably predict such changes will undoubtedly accelerate method development. Over the past five years or so, a substantial body of fundamental knowledge has been assembled (for example, effects of solvent gradient deformation and choice of scouting gradient conditions on the accuracy of retention models) that could now be leveraged in software designed for the purpose of supporting 2D-LC method development. It will be interesting to see if and when open-source or commercial solutions emerge in this area, and it will be exciting to see their impact on wider adoption of 2D-LC methodologies.
References
(1) L.R. Snyder, J.W. Dolan, and D.C. Lommen, J. Chromatogr. A 485, 65–89 (1989). https://doi.org/10.1016/S0021-9673(01)89133-0.
(2) J.W. Dolan, D. Lommen, and L.R. Snyder, J. Chromatogr. A 485, 91–112 (1989).
(3) L.M. Andrighetto, N.K. Burns, P.G. Stevenson, J.R. Pearson, L.C. Henderson, C.J. Bowen, and X.A. Conlan, Forensic Sci. Int. 266, 511–516 (2016). https://doi.org/10.1016/j.forsciint.2016.07.016.
(4) L.M. Andrighetto, P.G. Stevenson, J.R. Pearson, L.C. Henderson, and X.A. Conlan, Forensic Sci. Int. 244, 302–305 (2014). https://doi.org/10.1016/j.forsciint.2014.09.018.
(5) D.M. Makey, V. Shchurik, H. Wang, H.R. Lhotka, D.R. Stoll, A. Vazhentsev, et al., Anal. Chem. 93, 964–972 (2021). https://doi.org/10.1021/acs.analchem.0c03680.
(6) I.A. Haidar Ahmad, D.M. Makey, H. Wang, V. Shchurik, A.N. Singh, D.R. Stoll, I. Mangion, and E.L. Regalado, Anal. Chem. 93(33), 11532–11539 (2021). https://doi.org/10.1021/acs.analchem.1c01970.
(7) M. Sarrut, A. D’Attoma, and S. Heinisch, J. Chromatogr. A. 1421, 48–59 (2015). https://doi.org/10.1016/j.chroma.2015.08.052.
(8) B.W.J. Pirok, S. Pous-Torres, C. Ortiz-Bolsico, G. Vivó-Truyols, and P.J. Schoenmakers, J. Chromatogr. A 1450, 29–37 (2016). https://doi.org/10.1016/j.chroma.2016.04.061.
(9) S.R.A. Molenaar, P.J. Schoenmakers, and B.W.J. Pirok, More-Peaks, Zenodo (2021). https://doi.org/10.5281/ZENODO.5710442.
(10) M. Muller, A.G.J. Tredoux, and A. de Villiers, J. Chromatogr. A 1571, 107–120 (2018). https://doi.org/10.1016/j.chroma.2018.08.004.
(11) D.R. Stoll, K. Shoykhet, P. Petersson, and S. Buckenmaier, Anal. Chem. 89, 9260–9267 (2017). https://doi.org/10.1021/acs.analchem.7b02046.
(12) L.N. Jeong, R. Sajulga, S.G Forte, D.R. Stoll, and S.C. Rutan, J. Chromatogr. A 1457, 41–49 (2016). https://doi.org/10.1016/j.chroma.2016.06.016.
(13) D.R. Stoll, R.W. Sajulga, B.N. Voigt, E.J. Larson, L.N. Jeong, and S.C. Rutan, J. Chromatogr. A 1523, 162–172 (2017). https://doi.org/10.1016/j.chroma.2017.07.041.
(14) E. Tyteca and G. Desmet, J. Chromatogr. A 1361, 178–190 (2014). https://doi.org/10.1016/j.chroma.2014.08.014.
(15) E. Tyteca and G. Desmet, J. Chromatogr. A 1403, 81–95 (2015). https://doi.org/10.1016/j.chroma.2015.05.031.
(16) M.J. den Uijl, P.J. Schoenmakers, G.K. Schulte, D.R. Stoll, M.R. van Bommel, and B.W.J. Pirok, J. Chromatogr. A 1636, 461780 (2021). https://doi.org/10.1016/j.chroma.2020.461780.
(17) T.S. Bos, L.E. Niezen, M.J. den Uijl, S.R.A. Molenaar, S. Lege, P.J. Schoenmakers, G.W. Somsen, and B.W.J. Pirok, J. Chromatogr. A 1635, 461714 (2021). https://doi.org/10.1016/j.chroma.2020.461714.
(18) S.R.A. Molenaar, T.A. Dahlseid, G.M. Leme, D.R. Stoll, P.J. Schoenmakers, and B.W.J. Pirok, J. Chromatogr. A 1639, 461922 (2021). https://doi.org/10.1016/j.chroma.2021.461922.
(19) B.W.J. Pirok, D.R. Stoll, and P.J. Schoenmakers, Anal. Chem. 91, 240–263 (2019). https://doi.org/10.1021/acs.analchem.8b0.
(20) J. Boelrijk, B. Pirok, B. Ensing, and P. Forre, J. Chromatogr. A 1659, 462628 (2021). https://doi.org/10.1016/j.chroma.2021.462628
Dwight R. Stoll is with Gustavus Adolphus College, in St. Peter, Minnesota. Bob W.J. Pirok is an assistant professor in chemometrics and advanced separations at the Faculty of Science (FNWI) of the University of Amsterdam (UvA) and visiting professor at Gustavus Adolphus College in the group of Dwight Stoll. Direct correspondence to: dstoll@gustavus.edu.
