ICP-MS: When Sensitivity Does Matter

It makes intuitive sense — the higher the sensitivity of an inductively coupled plasma–mass spectrometry (ICP-MS) system, the lower the detection limit. But there are many factors that affect the detection limit for a given isotope in a given sample. These factors include sensitivity, background noise, and interferences.

In many applications in environmental management, semiconductor manufacture, and clinical research, some important elements are subject to spectral interferences. For the accurate determination of these elements, some form of interference management — collision reaction interface, collision cell, or reaction cell — often is employed.

With the recent focus on interference management techniques, less attention has been paid to one of the major benefits of inductively coupled plasma–mass spectrometry (ICP-MS) — a benefit that has spurred its growth over the past two decades. We are referring to sensitivity, the ratio of net signal to concentration. The importance of sensitivity should not be forgotten. Many elements of interest in many samples are not subject to significant spectral interference, and for such elements, the quantitation limit is set primarily by sensitivity.

Signal Noise, Sensitivity, and Detection Limits in ICP-MS

Detection limits for ICP-MS are quoted most often as "3 sigma" detection limits. These detection limits are derived using the following equation:

detection limit = (3 × σ_bl)/sensitivity

where the standard deviation of the blank (σ_bl) is expressed in counts per second, and the sensitivity is expressed in counts per second (cps) per unit concentration (ng/L).

This equation clearly shows the direct dependence of detection limits on sensitivity. In practice, the standard deviation of the blank also is affected by the sensitivity. This arises because part of the blank signal arises from traces of the element of interest. We go to a lot of trouble to avoid such contamination, but its complete elimination is not possible.

The total variation in background noise (σ_bl) is a combination of both source flicker noise (caused by instabilities in the operation of the nebulizer, spraychamber, and plasma, σ_sf) and Poisson or counting statistics noise (caused by the random nature of the arrival of ions at the detector, σ_cs) (2,3). Source flicker noise can be modeled as being a constant fraction of the total ion count rate, typically 0.5%. The counting statistics noise can be modeled as the square root of the average number of counts during a measurement:

σ_cs = √(average number of counts)

Practically, there is always some elemental contamination present in the analytical solutions. Assuming a constant low blank contamination, counting statistics (and hence, detection limits) on the blank count rate can be improved by increasing the sensitivity.

Table I shows the theoretical relationship between sensitivity, the two sources of background noise, and the resulting detection limit. For this example, it is assumed that there is a continuous background of 10 cps, a real blank signal arising from contamination of the blank with 1 ng/L of the element of interest, and that the integration time is 1 s. These results clearly show that counting statistics noise becomes more dominant as a proportion of the total noise as the count rate drops, and that the best detection limit is found when the sensitivity is greatest.

Table I: Theoretical calculations showing the effect of sensitivity on detection limits

In Table II, the same calculations have been done, but the assumed contamination of the blank has been reduced by a factor of 100, to 0.01 ng/L. The improvement in detection limit is greatest for the greatest sensitivity. The effect of background contamination is shown clearly when comparing Tables I and II. This reinforces the importance of a clean, controlled laboratory environment, high-purity reagents, clean laboratory ware, and stringent sample preparation procedures.

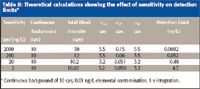
Table II: Theoretical calculations showing the effect of sensitivity on detection limits

Finally, in Table III, the assumed contamination of the blank remains at only 0.01 ng/L, and the continuous background has been reduced by a factor of 10, to 1 cps. The improvement in detection limit is greatest for the greatest sensitivity. Once again the benefit of high sensitivity is very clear.

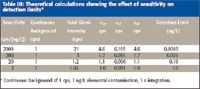
Table III: Theoretical calculations showing the effect of sensitivity on detection limits

Signal-to-Background Ratios and Detection Limits

Another common, and relatively simple, way of comparing sensitivity in ICP-MS is to look at the signal-to-background ratio (SBR) at a given mass. Often it is assumed that the higher the SBR, the better the performance (detection limit). However, this can be misleading. SBR is a valid measure of detection limits only when combined with a measure of the relative standard deviation of the background:

detection limit = (3 × σ_bl)/sensitivity = 3 RSD_b/SBR

If the background noise is dominated by source flicker noise, as it often was in the early days of ICP–optical emission spectrometry (OES), then RSD_b is approximately constant and the detection limit is inversely proportional to the SBR. The use of SBR in ICP-MS is evidently an inappropriate transfer of a concept that is sometimes valid in ICP-OES.

As is shown in Table IV, the detection limit clearly is improved by increasing the sensitivity — even when the SBR remains constant.

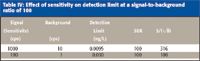
Table IV: Effect of sensitivity on detection limit at a signal-to-background ratio of 100

In ICP-MS, the background noise usually is dominated by counting statistics noise, and this is proportional to the square root of the background. A better guide to the effects of the signal and background on detection limits in ICP-MS is, therefore, the ratio of the signal to the square root of the background (S/[√B]). This parameter has been shown to be better than the SBR for optimizing modern ICP-OES instruments in which the background noise often is dominated by shot-noise, analogous to counting statistics noise in ICP-MS (4). The usefulness of the (S/[√B]) in ICP-MS is shown in Table IV. By comparing the S/(√B) of these two measurements, we can see that there is a 3.16-fold improvement (increase) in the ratio as we increase the sensitivity by a factor of 10. When we compare the detection limits, we also see an improvement (reduction) of 3.16-fold as we increase the sensitivity by a factor of 10.

In this example, for a constant SBR, we see improvement (reduction) in detection limit as we improve sensitivity, which is proportional to the improvement (increase) in S/(√B).

Factors Affecting Sensitivity

Sensitivity in ICP-MS is governed by many factors, including the design of the ICP-MS system (plasma system, plasma–mass spectrometer interface, ion optics, and quadrupole), the efficiency of the sample introduction system, and of course the instrument optimization conditions used (5,6).

Sensitivity for a given isotope also is dependent on its degree of ionization in the plasma, and its relative abundance. As an example, ²³²Th is close to 100% ionized in a typical ICP system (1) and has a natural abundance of 100%. In contrast, ¹⁹⁴Pt is only about 62% ionized (1) and has a natural abundance of only 32.9%. All else being equal, this means that the sensitivity for ¹⁹⁴Pt is only about 20% of that of ²³²Th.

Sensitivity of an isotope in ICP-MS often is normalized to millions of counts per second per part per million (Mcps/ppm, or Mcps/[mg/L]). Table V shows the relative sensitivity for ²³²Th and ¹⁹⁴Pt, and the number of counts per second of each when 1 ng/L of the element is present. Modern ICP-MS instruments range in sensitivity in this mass region from around 10 Mcps/(mg/L) up to 1000 Mcps/(mg/L) (7). The difference in sensitivity of these two isotopes is due primarily to difference in natural abundance and ionization in the plasma.

Table V: Relative sensitivity of 232Th and 194Pt

The Application of High Sensitivity ICP-MS

High sensitivity ICP-MS is useful in a range of applications including laser ablation, isotope ratio measurements, speciation, and measurement of isotopes in clinical research studies. The following example shows the practical use of high-sensitivity ICP-MS in the measurement of platinum anticancer drugs — an important class of chemotherapeutics (8).

The ability to measure platinum exposure in biological matrices is a prerequisite for understanding the pharmacokinetics of platinum anticancer agents. Little has been reported on the long-term retention of these drugs due to the reliance on atomic absorption techniques for the analysis of platinum. This technique lacks sufficient sensitivity for evaluating long-term platinum retention, but this shortfall can be overcome using a high-sensitivity ICP-MS system.

The increased sensitivity of ICP-MS makes it possible to study the behavior of these drugs over a significantly longer pharmacokinetic time scale. This will give better insight into the prolonged exposure to these drugs and the potential association with long-term side effects.

Figure 1 shows the three platinum compounds currently utilized extensively in chemotherapy.

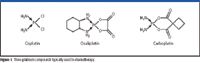
Figure 1

Plasma ultrafiltrate (pUF) is known to contain the pharmacologically active platinum fraction and hence, was chosen as the material for analysis. The determination of platinum in pUF presents several challenges. First, the sample size is small (typically 150 μL), so a significant dilution is required to provide adequate sample volume for analysis. This results in low Pt concentrations, particularly if effects of prolonged exposure are to be investigated. At these low levels, instrument sensitivity is paramount for successful long-term investigations.

Instrument and Optimization

A Varian 810-MS system (Palo Alto, California) was used with standard sample introduction system. A Varian SPS3 autosampler was used for automated analysis. All isotopes and masses of interest in this application are in the high mass region of the spectrum; as a consequence, the instrument was optimized for high mass response only. Sensitivity is paramount in this application — interferences are not a significant issue.

Typical sensitivities, oxide, and doubly charged ratios obtained from the MS system are shown in Table VI.

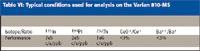
Table VI: Typical conditions used for analysis on the Varian 810-MS

Analysis and Preparation Environment

Because of the increased levels of Pt in our environment (for example, automotive catalytic converters and dental alloys), all measurements were carried out in a dedicated, temperature-controlled, positively pressurized environment. All solutions were prepared using plastic labware. All sample pretreatment devices were checked thoroughly for analyte, internal standard, and potential interfering elements.

Sample Treatment

Plasma was obtained by centrifuging whole blood samples for 5 min (3000 rpm, 4 °C).

pUF was obtained by centrifuging the plasma fraction through a 30-kDa cut-off ultrafiltrate filter (Centriplus YM-30, Millipore Corporation, Bedford, Massachusetts) for 15 min (3000 rpm, 20 °C).

Preparation of pUF was performed immediately after blood collection to prevent the decrease of free platinum levels.

Samples were stored at -20 °C until analysis.

Prior to analysis, pUF samples were thawed, vortex mixed, and diluted 100-fold. When samples contained platinum levels below 75 ng/L, they were diluted 10-fold.

Calibration Solutions

Chloroplatinic acid was used to prepare the calibration standards. This material is readily available in solution form, is certified, and is relatively harmless. The Pt anticancer agents are provided in the solid form and are toxic.

Before using this material in the calibration standards, its ability to be used to calibrate the concentration of the chemotherapeutic compounds was assessed, confirming that there was no analytical bias based upon the different chemical forms of Pt. All calibration standards were matrix matched in 1% pUF to the samples. Internal standard was spiked into the solutions. Chloroplatinic acid standards were prepared fresh daily, because experiments showed that Pt concentration of the solutions showed a decrease over time.

Isotope Selection and Detection Limit

Three isotopes of Pt were monitored, ¹⁹⁴Pt, ¹⁹⁵Pt, and ¹⁹⁶Pt. Potential oxide inferences from Hf were considered and judged to be insignificant. Isobaric overlap of ¹⁹⁶Hg with ¹⁹⁶Pt were corrected on line by monitoring ²⁰²Hg. ¹⁹⁴Pt/¹⁹⁵Pt and ¹⁹⁶Pt/¹⁹⁵Pt ratios were monitored as an indicator of unexpected interferences.

The ¹⁹⁴Pt isotope was used for all concentration determinations and validation calculations. The calibration range was 0.75 ng/L–100 ng/L in the 1% pUF matrix (0.75–100 ppt). A typical example of a calibration graph is shown in Figure 2.

Figure 2

Pt levels in the blank pUF used to prepare the standards were qualified before use. The upper concentration was limited to 100 ppt to minimize carryover and maintain a lower limit of quantification (LLOQ) of 0.75 ng/L (0.75 ppt) in 1% pUF.

On the basis of the data shown in the calibration graph, with a sensitivity of 205.9 cps/ppt, a 3σ detection limit of 0.049 ng/L (0.049 ppt) is achieved in the 100-fold diluted pUF, hence, 4.9 ng/L (4.9 ppt) in the undiluted pUF. Substituting the measured background (9 cps) and sensitivity (205.9 cps/ppt) into the theoretical calculation in Tables I–III gives a theoretical detection limit of 0.044 ng/L, which agrees well with the measured detection limit of 0.049 ng/L.

Clinical Application

Shown in Figure 3 are the results of the analysis of pUF samples of a subject who received 130 mg/m² oxaliplatin administered as a 2-h infusion.

Figure 3

Plasma samples were collected before the infusion and for up to three weeks after infusion. The inset graph is an expansion of the 0–5 h region of the graph.

Note that the concentration of platinum at three weeks is still above the LLOQ, indicating that the developed procedure is capable of long-term monitoring of Pt levels in pUF.

Conclusion

High-sensitivity ICP-MS is an important and useful tool for determining ultratrace levels of isotopes that do not suffer from significant spectral interference. For these isotopes, detection limits are improved when sensitivity is increased. Particular care also should be taken to keep background contamination of the analyte to a minimum, and to keep continuous background low.

SBR is not an accurate relative measure of performance in ICP-MS. A much better relative measure is the ratio of the signal to the square root of the background (S/[√B]).

A highly sensitive assay for the reliable and fast quantitative determination of platinum originating from cisplatin, carboplatin, and oxaliplatin in human pUF using ICP-MS was developed and subsequently validated according to current FDA guidelines. The validated range of determination was 75.0 ng/L to 1.00 × 10⁴ ng/L platinum in human pUF. By including a 10-fold dilution in the validation procedures in addition to the standard performed 100-fold dilution, the limit of quanitation was lowered to 7.50 ng/L. This is a 1.3–7-fold improvement on previous documented determination of Pt in pUF by quadrupole ICP-MS analysis and 2600-fold improvement on graphite furnace atomic absorption spectroscopy methods.

The assay now is applied successfully to long-term pharmacokinetic studies of subjects being treated with cisplatin, carboplatin, and oxaliplatin.

Shane Elliott, Barry Sturman, and Stephen Anderson are with Varian Australia Pty Ltd, Mulgrave, Victoria 3170, Australia.

Elke Brouwers and Jos Beijnen are with the Department of Pharmacy & Pharmacology, Slotervaart Hospital/The Netherlands Cancer Institute, Louwesweg 6, 1066 EC, Amsterdam, The Netherlands.

References

(1) R.S. Houk, Anal. Chem. 58, 97A–105A (1986).

(2) E. Denoyer, Atom. Spectroscopy 13, 93–98 (1992).

(3) J.D. Ingle, Jr. and S.R. Crouch, in Spectrochemical Analysis (Prentice-Hall, Englewood Cliffs, New Jersey, 1988), chapter 5 and pp. 245–246.

(4) D.A. Sadler, D. Littlejohn, and C.V. Perkins, J. Anal. Atom. Spectrom. 11, 207–212 (1996).

(5) I. Kalinitchenko, Ion Optical System for a Mass Spectrometer, United States Patent Number 6,614,021 B1 (2003).

(6) I. Kalinitchenko, "A New ICP-MS System," Winter Conference on Plasma Spectrochemistry, Frankfurt, Germany (2003).

(7) S. Elliott, M. Knowles, and I. Kalinitchenko, American Laboratory, 24–29 (March, 2004)

(8) E.E.M. Brouwers, M.M. Tibben, H. Rosing, M.J.X. Hillebrand, M. Joerger, J.H.M. Schellens, and J.H. Beijnen, J. Mass Spectrom. 41, 1186–1194 (2006).