Integration Problems

I recently received an e-mail inquiry from a reader, along with the two chromatograms shown in Figure 1. Although not explicitly stated in the e-mail, it was clear that a debate was raging about how to best integrate this group of peaks. Proper integration procedures is a topic that comes up with surprising regularity, so I would like to look at some aspects of integration in this month's "LC Troubleshooting."

John W. Dolan

The Best Approach

In Figure 1, it is possible to distinguish three peaks. Peak 1 is just a shoulder on the front of peak 2, whereas peaks 2 and 3 are distinct peaks. So the question is how to best integrate this set of three peaks to get results that are the most accurate — that is, most closely reflect the true area under the peaks. In Figure 1a, a valley-to-valley integration method is used. On the one hand, it may look like this is a good approach, but it misses peak 1 altogether. And, although the integrated area (above the drawn baseline) clearly belongs to peak 2 or peak 3, there is a gross under-integration of the two peaks. That is because all of the area beneath the integration line is ignored.

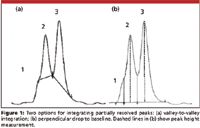
Figure 1

The correct way to integrate a group of peaks like this is to draw a perpendicular line from the valley between the peaks to the baseline extended between the normal baseline before and after the group of peaks, as seen in Figure 1b. For peak 1, it takes a bit of imagination to pick the correct point to drop the valley, and as we'll see in a minute, this is probably not appropriate anyway. For peaks 2 and 3, the process is simple. First draw a baseline connecting the real baseline before and after the peak group. Then draw a perpendicular line from the valley between each peak pair to the baseline.

The errors involved in the perpendicular drop method are as follows: If the peaks are approximately the same size, and tailing or fronting is ignored, the amount of the peak tail from the first peak (peak 2 in the present case) hiding under the second peak (peak 3) should be about the same as the amount of peak front from the second peak hiding under the first. If this is the case, the errors should cancel and peak areas should be fairly accurate. If the second peak fronts significantly or if the first peak has a strong tail, the weighting will be distorted, with corresponding errors. If the peak ratio is large — for example, 20:1 — the larger peak will be little affected by the minor contribution of the smaller peak, but the smaller peak will have excess area contributed by the major peak. In this case, the accuracy for the larger peak should be much better than for the minor peak. When the resolution between the peaks is so small that a clear valley is not present, as in the case for peak 1 in this example, the perpendicular drop will grossly over-integrate the peak. A peak skim is more appropriate for integration of peak 1; see further discussion of Figure 2b below.

Figure 2

A related question is when, if ever, is it appropriate to use a valley-to-valley integration technique? The simple answer is that if a known baseline disturbance is present under a set of eluted peaks, valley-to-valley may be appropriate. In the case of Figure 1a, there would have to be a large, broad peak that is roughly defined by the area under the drawn baselines. This is unlikely to occur, and I can never remember encountering such a situation in my experience in the laboratory. On the other hand, in some gradient runs, there may be a small, broad rise in the baseline of blank runs that is consistent enough to allow valley-to-valley integration. In this case, however, the valleys between peaks should reach nearly to the baseline extended from before to after the peak group. This is also a rare occurrence, so the bottom line here is that valley-to-valley integration seldom is the best approach.

Other Common Errors

While the valley-to-valley problem mentioned previously may not be encountered often, there are other integration errors that may be more common. I've shown three of these in Figure 2. In Figure 2a, the data system chose to draw the baseline (solid line) from the bottom of the dip before the peak to the baseline after the peak. This is a result of the default integration mode of connecting the baseline (lowest point) before and after the peak. The problem, of course, is that the negative peak just before the peak of interest is falsely identified as true baseline. The correct integration is shown with the dashed line. The area above the dashed line and within the peak envelope better represents the true peak area than the original integration.

A different example of the slightly resolved peak 1 of Figure 1 is shown in Figure 2b. Here a small but distinct peak appears on the tail of the major peak. The data system chose a perpendicular drop to the extended horizontal baseline as the integration technique. It is easy to see in this case that the tail of the first peak extends under the minor second peak. The perpendicular drop will under-report the area for the large peak and over-report the area for the smaller one. The proper integration technique is to skim the smaller peak off the tail of the larger one, as shown by the dashed line. I've heard debates about whether this skim line should be linear (a tangent skim) or curved (an exponential skim) or some other shape. This may be of academic interest, but it is of little practical interest. Whenever a skim is used, it is merely an estimate of the peak area (see the conclusions at the end of this column) — consistency of integration methodology is more important than whether the skim is a tangent or curved. As a rule of thumb, if the minor peak is <10% of the height of the major one, skimming the peak is the appropriate integration technique. If the minor peak is >10% of the height of the major one, a perpendicular drop to the baseline connecting the true baseline before and after the peak group is best.

Another very common integration error is shown in Figure 2c. Here the baseline after the peak is falsely located before the peak descends to the true baseline. The data system identifies the start and end of the peak by determining if the signal is rising (or falling) faster than the baseline would in the absence of the peak. This means that determining the end of the peak is especially problematic when the peak tails strongly, the peak is small, and the baseline drifts. When this situation exists, not only can the peak be integrated improperly, but also, the peak endpoint may vary significantly from one run to the next. The proper integration for Figure 2c is shown by the dashed line. One way to help avoid the problem of identifying a false peak-endpoint before the peak has been fully eluted, is to force the peak end to some point after you are sure the peak will reach the baseline. For example, in Figure 2c, this point could be where the peak-end is located with the dashed integration line or even a little to the right of that. Erroneously marking the peak end too late may have little practical effect, because the additional area created usually is a very small contribution to the overall peak area and, thus, a small contribution to integration error.

Improving Peak Appearance

If most of your experience is with UV or fluorescence detection and with peaks that are distinct on the baseline, the problems identified in Figures 1 and 2 will likely be the most common integration problems you encounter. If you switch to tandem mass spectrometric detection (MS-MS), however, you may be surprised at the results — I know that I was when I first encountered liquid chromatography (LC)–MS-MS. Figure 3a shows a typical chromatogram of the raw signal at the lower limit of quantification (LLOQ) for a method to determine a drug in plasma. The first peak is a metabolite and the second peak comprises the analyte and co-eluted ¹³C internal standard. I remember my first reaction to seeing such peaks: something is wrong here! But this is not at all the case. With the MS-MS instrument, at least in theory, because the electrometer counts ions exiting the third quadrupole, there is either a signal present or not. The magnitude of the signal will vary across the peak according to the concentration of the peak and the superimposed noise. When each data point is connected to the next, ragged peaks, such as in Figure 3a, are seen. The big question here is how to integrate the peaks. The baseline is noisy, but drawing an integration baseline through the middle of the noise to connect the true baseline before and after the peaks is not too challenging. The problem arises with where to locate the top of the peak. The solution to the problem is to smooth the peak. Peak smoothing applies a signal-averaging algorithm that averages the adjacent points to give a more pleasing peak appearance that is easier to integrate. If done properly, as is the case for Figure 3b, the peaks appear much more "normal" and accurately reflect the true peak area when integrated properly. Over-smoothing can compromise the signal, so care needs to be taken to avoid this.

Figure 3

What About Peak Height?

Before the advent of modern data systems, there was regular discussion about whether peak height or peak area was a more accurate way to quantify a peak. With manually measured peaks, peak area was estimated by triangulating the peak between points on the baseline at the beginning and end of the peak and at its apex. This meant three measurements, plus the assumption that the peak is a triangle, when it more closely represents a Gaussian distribution. Three measurements meant more error than the two required for the perpendicular height (apex and baseline), so it was argued that height was a better choice. Those arguments are somewhat moot today, because all data systems measure the peak as area or height slices from the baseline to each point along the peak. The height is the largest of these slices and the area is the sum of the slices. Most of the time, peak area will give better results because it inherently averages error across the peak, but area is not always the best choice.

In Figure 1b, the peak height for peaks 2 and 3 is shown by the vertical dashed line. When two or more peaks overlap, as in Figure 1, peak height may be a better choice than peak area. If you were to draw the tail of peak 2 and the front of peak 3 to baseline, you would conclude that there is very little overlap at the center of the peaks where the peak height is measured. This would be expected to give less error than peak area, where there is known overlap.

On the other hand, peak height for peaks such as those in Figure 3a would be expected to have a much greater probability of picking a false peak maximum than peak area, which averages out the noise across the peak. So peak area would be the preferred technique here. With the smoothed signal, the difference would not be expected to differ as much.

The simplest way to determine the best integration technique is to run a set of known samples, such as during or before validation and collect data for both peak height and area. Calculate the results using both techniques and use the method that gives the most accurate and precise results.

Is Hand-Integration Legitimate?

Another common question that I get regarding integration is the complaint that goes something like, "My boss won't let me adjust integration baselines in the chromatogram. He insists that the data system must be set to integrate all peaks properly and that the regulatory agencies will not allow manual baseline adjustments." This may be a fine argument for well-behaved methods with well-resolved peaks and negligible baseline noise, for example, content uniformity or potency tests for drug substance or drug product. However, whenever trace analysis is involved, such as impurities methods, drugs in plasma, or pesticides in the environment, peak integration can be much more challenging. As the peak gets smaller, the signal-to-noise ratio (S/N) gets smaller and it is harder for the integrator to find the true baseline. This is shown for the large peak of Figure 2c, and it is easy to imagine that the difficulty increases as the peak size decreases and baseline noise and drift increase. In the laboratory I was most recently involved with, we had a process we called "peer review," where after the analyst had finished integrating the chromatograms, they were reviewed by someone else before going to the quality group, at which point the data were "locked down" and integration changes required additional documentation. In this system, I reviewed thousands of chromatograms from hundreds of batches of samples, many of which were at or near the LLOQ. Of these, my guess is that less than a dozen did not require some manual integration. While the data systems today do a good job of integration, they are not perfect.

To protect against frivolous reintegration or adjusting baselines so that the results meet a desired result, the FDA has a guideline commonly referred to as "21 CFR Part 11," "Part 11," or just "Electronic Signatures Rules" (1). This guideline states that if manual integration is performed, four criteria must be met: the original "raw" data must be preserved for later inspection, the person who made the change must be identified, the time and date of change must be noted, and the reason for the change must be recorded. Nearly every data system available today has an "audit trail" feature that complies with these regulations. A copy of the original data is archived. Because the user must sign on to the computer to use it, the username, date, and time are automatically stamped on each event. The software prompts for an explanation for each manual integration event. For example, the correction of the baseline in Figure 2c might be noted as "wrong baseline end." So the bottom line here is that the regulatory agencies anticipate that manual integration will be required and have set down guidelines to follow in such cases. If these guidelines are followed, you should not worry about negative regulatory action when you manually integrate a chromatogram to correct an error by the data system.

Conclusions

In my experience, modern data systems do a marvelous job of integration in most cases. My recommendation is to allow the data system to integrate several typical samples and let it determine how to set the integration parameters. Then inspect the results and decide if they are satisfactory. If you encounter problems, such as those illustrated Figures 1 and 2, you may want to set the integration parameters to force particular integration techniques for certain peaks in the chromatogram. However, no matter how carefully you set up the data system, it is unlikely that it will pick all the peaks properly every time. You should visually inspect every chromatogram produced by your LC system to be sure it is integrated properly, and adjust the integration if necessary.

Want more information on integration? Look in your data system manual or try reference 2. This book contains nearly 200 pages of information about integration — much more than most people ever want to know. However, my copy is loaded with sticky notes marking practical advice. One of my favorite statements in the book, very loosely quoted, is to the effect that chromatography always trumps integration. In other words, you can try all sorts of tricks to get a useable area from peak 1 of Figure 1 or the second peak of Figure 2b, but you will never get results as good as those obtained if you had a better LC separation. Integration of poorly resolved peaks is only an estimate of the more accurate results you would get when the peaks are baseline resolved.

John W. Dolan "LC Troubleshooting" Editor John W. Dolan is Vice-President of LC Resources, Walnut Creek, California; and a member of LCGC's editorial advisory board. Direct correspondence about this column to "LC Troubleshooting," LCGC, Woodbridge Corporate Plaza, 485 Route 1 South, Building F, First Floor, Iselin, NJ 08830, e-mail John.Dolan@LCResources.com.

For an ongoing discussion of LC trouble-shooting with John Dolan and other chromatographers, visit the Chromatography Forum discussion group at http://www.chromforum.org.

References

(1) Guidance for Industry: Part 11, Electronic Records; Electronic Signatures – Scope and Application, USFDA-CDER, Aug. 2003, http://www.fda.gov/ora/compliance_ref/part11.

(2) N. Dyson, Chromatographic Integration Methods, 2nd ed. (Royal Society of Chemistry, Letchworth, UK, 1998).