Where Has My Efficiency Gone? Impacts of Extracolumn Peak Broadening on Performance, Part III: Tubing and Detectors

Dispersion (broadening, or spreading) of analyte zones (peaks) outside of chromatography columns can seriously erode the resolution that good columns provide. In this installment, we focus on the contributions of dispersion in connecting tubing and detectors to the total level of extracolumn dispersion in a LC system.

In the installments of “LC Troubleshooting” from the last two months, we reviewed the basic concepts of extracolumn dispersion (ECD) (1), mentioned how the level of ECD associated with a particular instrument can impact the apparent quality of a separation (for example, as measured by resolution), and discussed dispersion associated with the injection step in some detail (2).

In this month’s installment, we continue our discussion of details associated with the contributions of specific system components. Figure 1 illustrates the contributions of different system components to the total observed variance, starting with the injection step and ending with the detection step. In principle, the total observed peak variance is simply the sum of the variances contributed by each system component. This is only rigorously correct if the dispersion in each element of the system is independent of the others (3), but under most conditions, equation 1 is accurate enough to guide method development and system optimization (4). In this installment of “LC Troubleshooting,” we continue by discussing dispersion in connecting tubing and detectors.

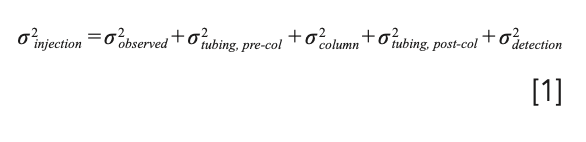
FIGURE 1: Illustration of the contributions of several LC system components to the total variance of peaks observed at the detector, σ²_observed. We note that equation 1 is valid using either time- or volume-based variances.

Dispersion in Connecting Tubing

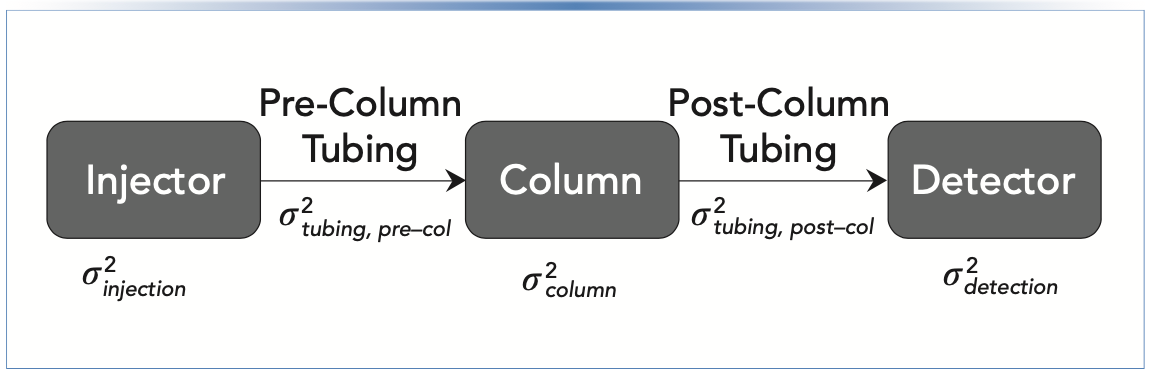
It is a well known fact that increasing the length and inner diameter of connecting capillaries in a chromatographic instrument increases dispersion. This dispersion is the result of the parabolic flow profile that is established in an open capillary under laminar flow conditions. Under these conditions, the fluid in the center of the tube moves at twice the average velocity, whereas the fluid near the wall is stagnant (that is, stuck to the wall). Estimating the contribution of this dispersion that occurs in connecting capillaries to the total extracolumn band broadening in a liquid chromatography (LC) system is not straightforward. The two limiting conditions for which analytical solutions exist are as follows: 1) dispersion in a short, straight capillary at high-flow rates (with negligible radial equilibration between velocity streams); and 2) dispersion in very long capillaries at low-flow rates (that is, where full radial equilibration between velocity streams occurs by diffusion). In the first case, the dispersion contribution of the capillary is given by the Atwood-Golay equation below (5):

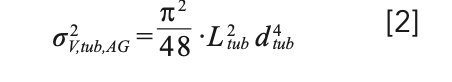
where L_tub and d_tub are the length and diameter of the capillary, respectively. In the second case, the dispersion is given by the Taylor-Aris equation, where F is the flow rate through the capillary and D_m is diffusion coefficient of the analyte in the mobile phase (6).

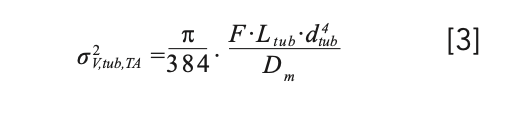
Most conditions used for practical LC methods lie between the extreme conditions where equations 2 and 3 are valid, and thus require that we consider a partial radial equilibration of the analyte across the tubing diameter (that is, across different mobile phase velocity streams). For this purpose, we can use either a Giddings-style coupling of the previous expressions (equation 4) (7), or an exponential model based on numerical simulations (equation 5) (8):

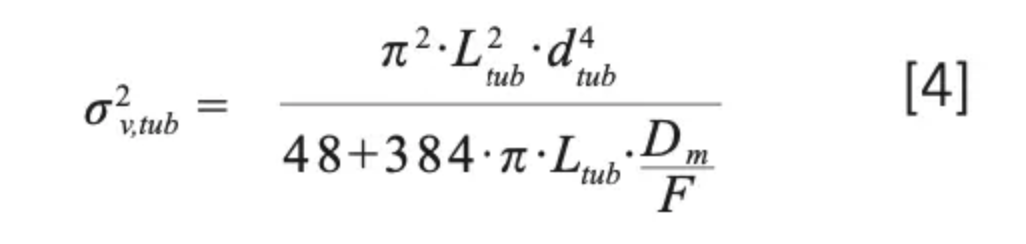
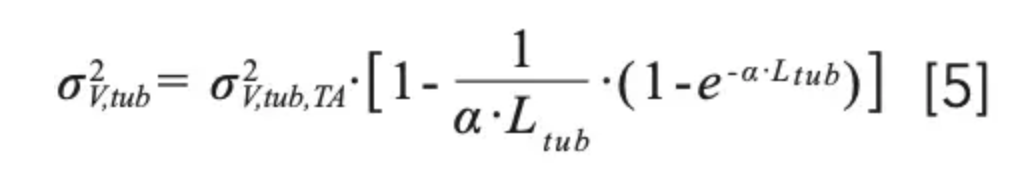
with α given by α = 15.04^.π^.D_m/F. In practice, however, equations 4 and 5 both seem to overestimate the degree of dispersion due to these capillaries in comparison to experimental observations, especially at high flow rates (7). One possible explanation for this observation comes from the fact that these equations are only valid for a straight tube, which is seldom used in real instruments where the capillaries are coiled and bent to fit in different instrument components, such as the injection valve, mobile phase preheaters, the column, and the detector inlet. As a result of this coiling, centripetal forces acting on the liquid cause secondary radial flow effects in the liquid. Beyond a critical flow rate, these radial flow effects are pronounced enough to enhance radial mixing and thus the equilibration of the analyte across the diameter of the tube. This in turn relaxes the axial dispersion that normally results from the parabolic flow profile. Nevertheless, equations 2–5 make it clear that using shorter and narrower capillaries reduces contribution of these tubes to the total extracolumn dispersion. This is especially true when using gradient elution, where the volumes of peaks exiting the column are typically much smaller than they are when using isocratic elution. Figure 2 shows that even for a relatively short (140 mm) piece of tubing between the column outlet and the detector inlet, the diameter of this tube can have a dramatic effect on peak width observed at the detector (3). When considering the use of narrow capillaries, however, one must be cautious about the pressure required to push the mobile phase through these tubes at the desired flow rate (ΔP_tub), because this increases along with the inverse fourth power of the column diameter as shown in equation 6 below (where η is the dynamic viscosity of the mobile phase).

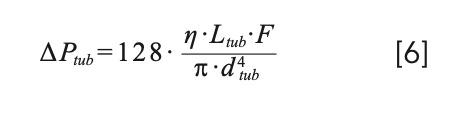
FIGURE 2: Example of the effect of post-column tubing diameter (L_tub = 140 mm in each case) on peak width and height in the case where gradient elution is used. The x-axis is effective retention factor ([t_R-t_m]/t_m). The column used was 50 mm x 2.1 mm i.d. (1.3 μm particles), the analyte was benzophenone, and the flow rate was 0.6 mL/min. Adapted from reference (4).

For example, changing from a commonly used 120 μm i.d. stainless steel capillary to a 75 μm i.d. capillary comes at the cost of a 6.5-fold higher pressure drop.

Dispersion in Detectors

Because of the widespread use of UV absorbance detectors in LC, most investigations into the contributions of detectors to extracolumn dispersion have been focused on UV detectors, although most fundamental aspects can also be applied to other types of detectors with flow-through detection cells. In a first, rough approximation, these flow cells behave as open-tubular flow paths that are either circular or rectangular in cross-section. As a result, the equations that govern dispersion in circular tubes can be used to estimate their contributions to extracolumn dispersion. However, the entire fluidic path in a detector module is more than the detection cell itself, and often involves additional in- and outlet tubing, sharp turns, and changes in the cross-sectional area or shape of channels. Nevertheless, in the literature, the volumetric variance of dispersion attributed to the detector has often been related to the geometrical detection cell volume (V_cell) using an empirical relationship similar to that of the injection volume contribution (2).

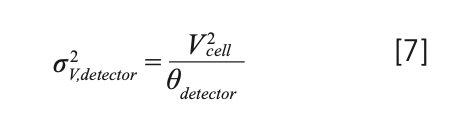
The proportionality between cell volume and dispersion is not surprising because equations 2–5 show that a longer or broader flow path results in more dispersion. Thus, there is a tradeoff between dispersion and sensitivity during flow cell design because longer flow cells result in higher sensitivity (9), and broader cell design reduces signal noise. This is illustrated in Figure 3, which shows how narrower peaks are obtained using the flow cell with the smaller volume; however, this comes at the cost of reduced sensitivity (that is, lower peak height) and a much higher baseline noise level. Innovations in the fluidic and optical characteristics of these cells over the past decades have enabled improvements in sensitivity (higher) and noise (lower), while maintaining or decreasing flow cell volume.

FIGURE 3: Comparison of peak width and baseline noise for UV flow cells with different volumes. (a) Inset shows the pre-peak region where the baseline noise is obviously much worse for the smaller flow cell. Note that the peak heights before normalization were about 360 and 560 mAU for the 80 and 500 nL flow cells, respectively. Adapted from reference (3).

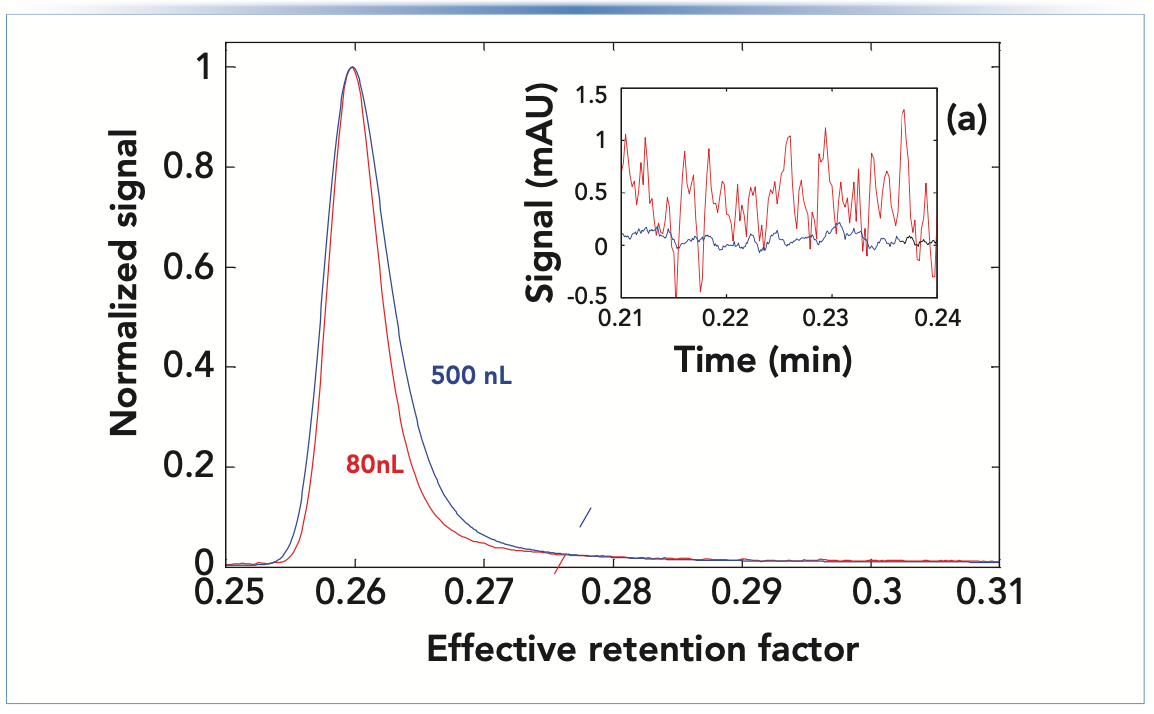
Recent studies have shown that equation 7 provides poor estimates of the actual contributions of flow-through cells to the total extracolumn dispersion (10,11). As was discussed for the injection step (2), if a rectangular plug of analyte would move through the detector flow cell in a perfect plug flow without mixing, θ_detector would be 12. On the other hand, if the flow cell would behave as a “perfect mixer”, θ_detector would be 1. However, if there are zones in the flow cell that are poorly swept because of flaws in the cell design, then values of θ_detector below 1 can be observed (10).

In addition, another consequence of the similarities between dispersion in a flow-through cell and dispersion in a capillary is that dispersion in the flow cell is expected to be flow rate dependent. Using a custom detector that allowed continuous variation of the cell pathlength, Dasgupta and others also showed that for short cell path lengths, the in- and outlet connections to the illuminated part of the flow cell make up the majority of the measured dispersion (10). To a first approximation, the dispersion at higher flow rates, typically above 0.5 mL/min, from modern low volume flow cells can be estimated using equation 7 with θ_detector = 0.5–0.8 (11). Given the fact that the dispersion of a flow cell is significantly affected by its internal design, some instrument vendors no longer report the geometrical cell volume, and instead report the expected contribution of the flow cell to peak widths (11).

In discussions on dispersion associated with detectors it is important to note that settings associated with the electronic components of the detector (for example, sampling frequency, and detector rise time or time constant) can also affect peak width and shape. Although strictly speaking these do not contribute to extracolumn dispersion in the same way as the other factors we have discussed (for example, detector cell volume), the effects of these settings can influence the observed peak variance and be confused with other contributions. Readers interested in learning more about this topic are referred to prior “LC Troubleshooting” articles (12), and some recent journal articles on the topic (13,14).

Finally, even though mass spectrometric (MS) detection is being used in more and more laboratories, there are far fewer studies of the contributions of MS detectors to extracolumn dispersion than there are for UV detectors (15,16). In the studies that have been done, however, it was found that when optimized MS settings are used, the ionization source and MS detector itself had little impact on observed peak widths. In fact, it was found that the tubing connecting the LC instrument to the mass spectrometer (MS) was the most critical contributor to the extracolumn dispersion for these hyphenated systems.

Summary

In this installment of “LC Troubleshooting,” we have continued our discussion of details associated with the contributions of specific LC system components to extracolumn dispersion, this time focusing on connecting tubing and detectors. In the next installment in this series, we discuss how the impact of extracolumn dispersion can be different under isocratic and gradient elution conditions, and discuss the impact of post-column flow splitting on the total dispersion observed at the detector.

References

(1) D. Stoll and K. Broeckhoven, LCGC N. Am. 39, 159–166, (2021).

(2) D. Stoll and K. Broeckhoven, LCGC N. Am. 39, 208–213 (2021).

(3) G. Desmet and K. Broeckhoven, Trends Anal. Chem. 119, 115619 (2019). https://doi.org/10.1016/j.trac.2019.115619

(4) K. Vanderlinden, K. Broeckhoven, Y. Vanderheyden, and G. Desmet, J. Chromatogr. A 1442, 73–82 (2016). https://doi.org/10.1016/j. chroma.2016.03.016

(5) M.J.E. Golay and J.G. Atwood, J. Chromatogr. A. 186, 353–370 (1979). https://doi.org/10.1016/S00219673(00)95261-0

(6) R. Aris, Proc. R. Soc. Lond. A. 235, 67–77 (1956). https://doi.org/10.1098/rspa.1956.0065

(7) K.J. Fountain, U.D. Neue, E.S. Grumbach, and D.M. Diehl, J. Chromatogr. A. 1216, 5979–5988 (2009). https://doi.org/10.1016/j.chroma.2009.06.044

(8) K. Broeckhoven and G. Desmet, J. Chromatogr. A 1216, 1325–1337 (2009). https://doi.org/10.1016/j.chroma.2008.12.065

(9) M. Dong and J. Wysocki, LCGC N. Am. 37, 750–759 (2019).

(10) P.K. Dasgupta, C.P. Shelor, A.F. Kadjo, and K.G. Kraiczek, Anal. Chem. 90, 2063–2069 (2018). https://doi. org/10.1021/acs.analchem.7b04248

(11) K. Vanderlinden, G. Desmet, and K. Broeckhoven, Chromatographia 82, 489–498 (2019). https://doi.org/10.1007/s10337-018-3622-1

(12) J.W. Dolan, LCGC N. Am. 14, 378–380 (1996).

(13) M.F. Wahab, P.K. Dasgupta, A.F. Kadjo, and D.W. Armstrong, Analytica Chimica Acta. 907, 31–44 (2016). https://doi.org/10.1016/j.aca.2015.11.043.

(14) A. Felinger, A. Kilár, and B. Boros, Analytica Chimica Acta. 854, 178–182 (2015). https://doi.org/10.1016/j.aca.2014.11.014.

(15) D. Spaggiari, S. Fekete, P.J. Eugster, J.-L. Veuthey, L. Geiser, S. Rudaz, and D. Guillarme, J. Chromatogr. A 1310, 45–55 (2013). https://doi.org/10.1016/j.chroma.2013.08.001.

(16) S. Buckenmaier, C.A. Miller, T. van de Goor, and M.M. Dittmann, J. Chromatogr. A 1377, 64–74 (2015). https://doi.org/10.1016/j.chroma.2014.11.086.

ABOUT THE AUTHORS

Ken Broeckhoven received his PhD in 2010 from the Vrije Universiteit Brussel (VUB), in Brussels, Belgium. Following post-doctoral research at VUB and work as a visiting researcher in the separation processes laboratory at ETH Zurich, in Switzerland, he became a research professor at VUB in 2012. He was subsequently promoted to Assistant Professor and then to his current position as an Associate Professor in 2017.

ABOUT THE COLUMN EDITOR

Dwight R. Stoll is the editor of “LC Troubleshooting.” Stoll is a professor and the co-chair of chemistry at Gustavus Adolphus College in St. Peter, Minnesota. His primary research focus is on the development of 2D-LC for both targeted and untargeted analyses. He has authored or coauthored more than 75 peer-reviewed publications and four book chapters in separation science and more than 100 conference presentations. He is also a member of LCGC’s editorial advisory board. Direct correspondence to: LCGCedit@mmhgroup.com