Where Has My Efficiency Gone? Impacts of Extracolumn Peak Broadening on Performance, Part 4: Gradient Elution, Flow Splitting, and a Holistic View
Dispersion (broadening, or spreading) of analyte zones (peaks) outside of chromatography columns can seriously erode the resolution provided by good columns. In this final instalment of the series we focus on the impact of elution mode (isocratic or gradient) and postcolumn flow splitting on the total level of extracolumn dispersion (ECD) in a liquid chromatography (LC) system, and demonstrate the use of a free, web-based calculator that can be used to guide decision making aimed at reducing ECD during method development.
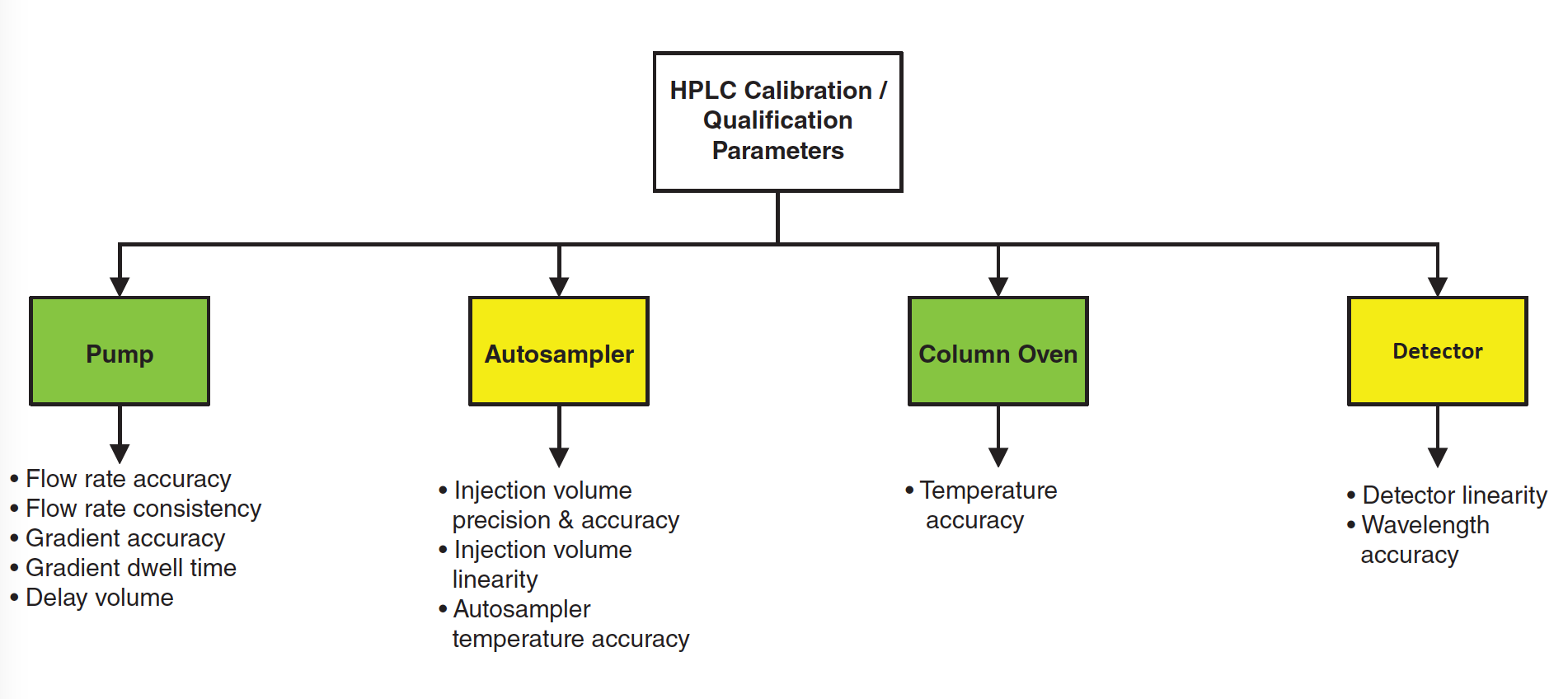
In the three instalments of “LC Troubleshooting” published in May, June, and July 2021 we reviewed the basic concepts of extracolumn dispersion (ECD) (1), and discussed the contributions of the injection step (2), connecting tubing, and spectroscopic detectors (3) to the total observed variance in some detail. In this month’s instalment, we conclude our discussion of specific contributions to the total variance by addressing how elution mode (that is, isocratic or gradient elution) affects the total level of ECD, and how postcolumn flow splitting can affect the observed variance. Finally, we demonstrate the use of a free, web‑based calculator that leverages the theory discussed in these instalments to enable quick and easy estimation of the magnitudes of the different contributions to the total observed variance.
Extracolumn Dispersion under Gradient Elution Conditions
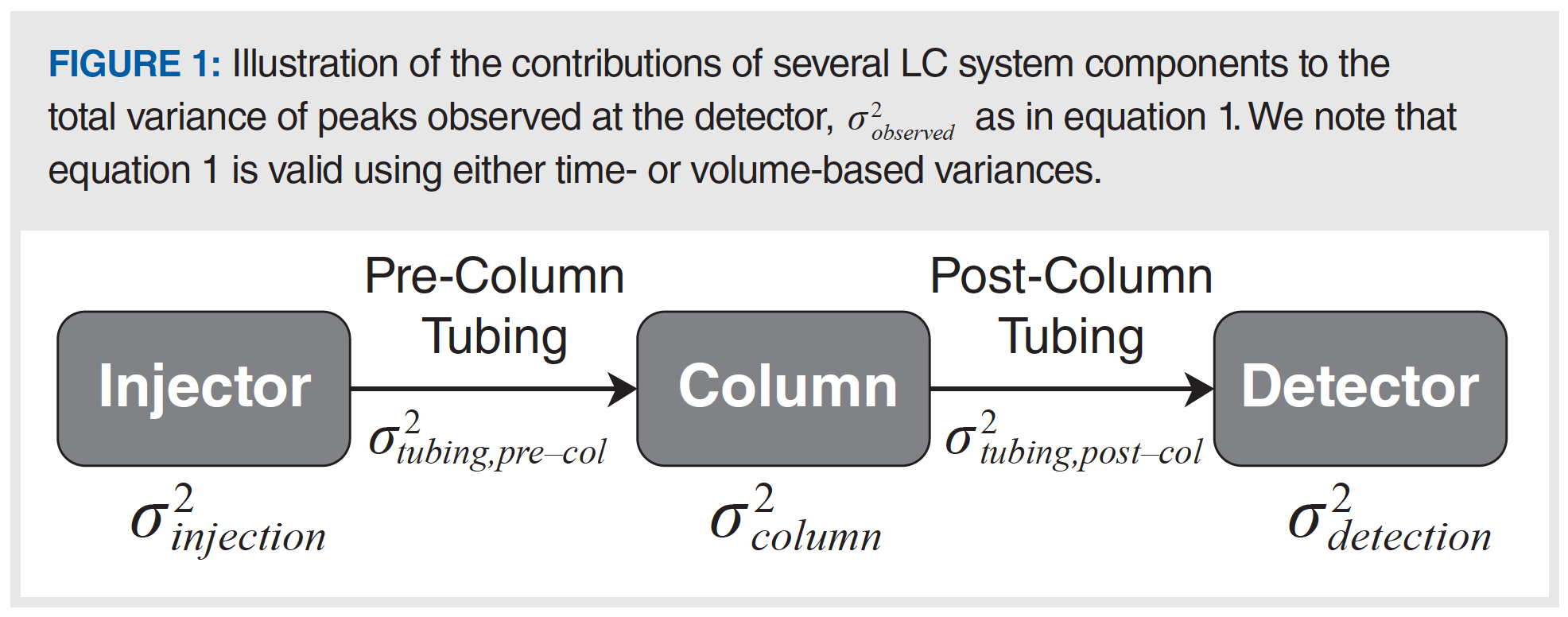
Figure 1 illustrates the different contributions to the total observed peak variance σ2obs . Equation 1 is most relevant when isocratic elution is used, and the solvent composition of the sample matches that of the mobile phase. When this is not the case, then variants of equation 1 are more relevant, where the magnitude of specific contributions to the total variance are either increased or reduced, depending on the specific conditions.
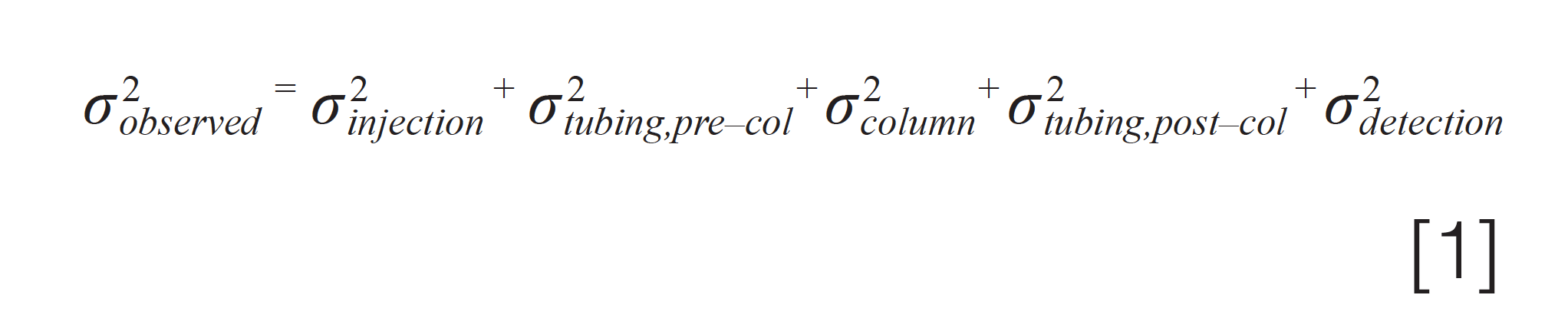
For example, in Part 2 of this series, we discussed how the impact of the σ2injection
term can be reduced by employing different “tricks” during the injection step, including preparing the sample with a low concentration of “strong solvent” compared to the mobile phase composition, and so-called “sandwich injection”. When gradient elution conditions are used, there is the potential to significantly reduce all of the precolumn contributions to the total variance, including the injection and precolumn tubing components. This effect is especially pronounced in cases where the gradient is started at a mobile phase composition that is “weak” relative to the mobile phase composition that an analyte is eluted in (for example, in reversed-phase LC, a low concentration of organic solvent in the mobile phase), and the injected sample also contains a low concentration of “strong” solvent.
In these cases, the precolumn contributions to the total variance are very small because any dispersion of the analyte that occurs upstream from the column inlet is effectively “undone” as the analytes all adsorb to the stationary phase at the column inlet and form a very narrow analyte band in the column. This is typically referred to as “focusing” of the analyte at the column inlet. Although this is a fortunate outcome when the separation conditions allow it, this type of outcome is not inevitable, and there are certainly cases where a relatively large injected volume of a sample containing a high concentration of strong solvent can lead to serious peak broadening, even if gradient elution is used (4).
When conditions are favourable for reduction in the precolumn contributions to ECD, the postcolumn contributions suddenly become more important. This is both because the precolumn contributions to ECD are minimized, and because peak volumes in gradient elution tend to be smaller and more uniform compared to those observed in isocratic separations (see equation 3 of Part 1 of this series [1]; for gradient separations, k is replaced with ke, the local retention factor at the column exit, which is about 1–3 for most separations). In the case of connecting tubing in particular, reducing the tubing diameter is especially tempting because of the strong fourth-power dependence of this variance contribution on the diameter, and reducing the tubing length is often limited by the physical proximity of instrument components such as the column and detector. However, we should choose tubing diameters carefully, because the pressure required to drive mobile phase through these small tubes also increases strongly with decreasing tubing diameter. Under conditions of optimal particle size and column length, a total pressure of 1500 bar, and gradient elution, Broeckhoven and Desmet found that the optimal postcolumn tubing diameter roughly doubled from 60 to 120 µm internal diameter (i.d.) for target efficiencies of 10,000 or 500,000 plates, respectively (5).
Effect of Postcolumn Flow Splitting on Dispersion
Postcolumn flow splitting is common in contemporary LC work, especially when a mass spectrometric (MS) detector is coupled with an LC separation executed at a higher flow rate than the MS instrument can tolerate. Important applications that involve these conditions are high-throughput methods, and two-dimensional LC where flow rates in excess of 0.5 mL/min are frequently used in the second dimension to improve the throughput of that part of the separation. Although sophisticated active splitting devices are sometimes used to control the split ratio, the most common approach is to use a simple tee-piece with different lengths and diameters of tubing at the two outlet branches of the tee to control the split ratio. However, in spite of the importance of these applications, the contribution of the flow splitting step to ECD has been the focus of only a few systematic studies published in the literature. We have recently published one of these studies, which was motivated by our frequent observation that peaks were wider than we expected when using postcolumn flow splitting (6).
During the course of this study, our principal realization was that postcolumn flow splitting can lead to peak volumes exiting the split point that are very small (for example, much less than 1 µL) compared to those encountered in all other analytical‑scale LC separations. This concept is illustrated in Figure 2. These low-volume post-split peaks are then highly susceptible to broadening by dispersion in all of the system elements downstream from the split point, which are typically connecting tubing and the detector. In our work, we did not find any evidence that the splitting process (for example, what happens in the tee piece itself) contributes significantly to the overall variance. Thus, estimation of the impact of the post-split elements is pretty straightforward. The volume of a peak exiting the split point
(σv,post–split) is determined by the ratio of the flow rate through the column (Fcolumn) and the flow rate exiting the split point (Fpostsplit ), as in equation 2. Then, the total variance observed at the detector (σv,obs = σt2,obs ∙ F2post–split) is the sum of the post-split tubing and detector variances (see [2] for tubing and detector variances), where the pre-split variance includes contributions from the injector, and pre- and postcolumn tubing.
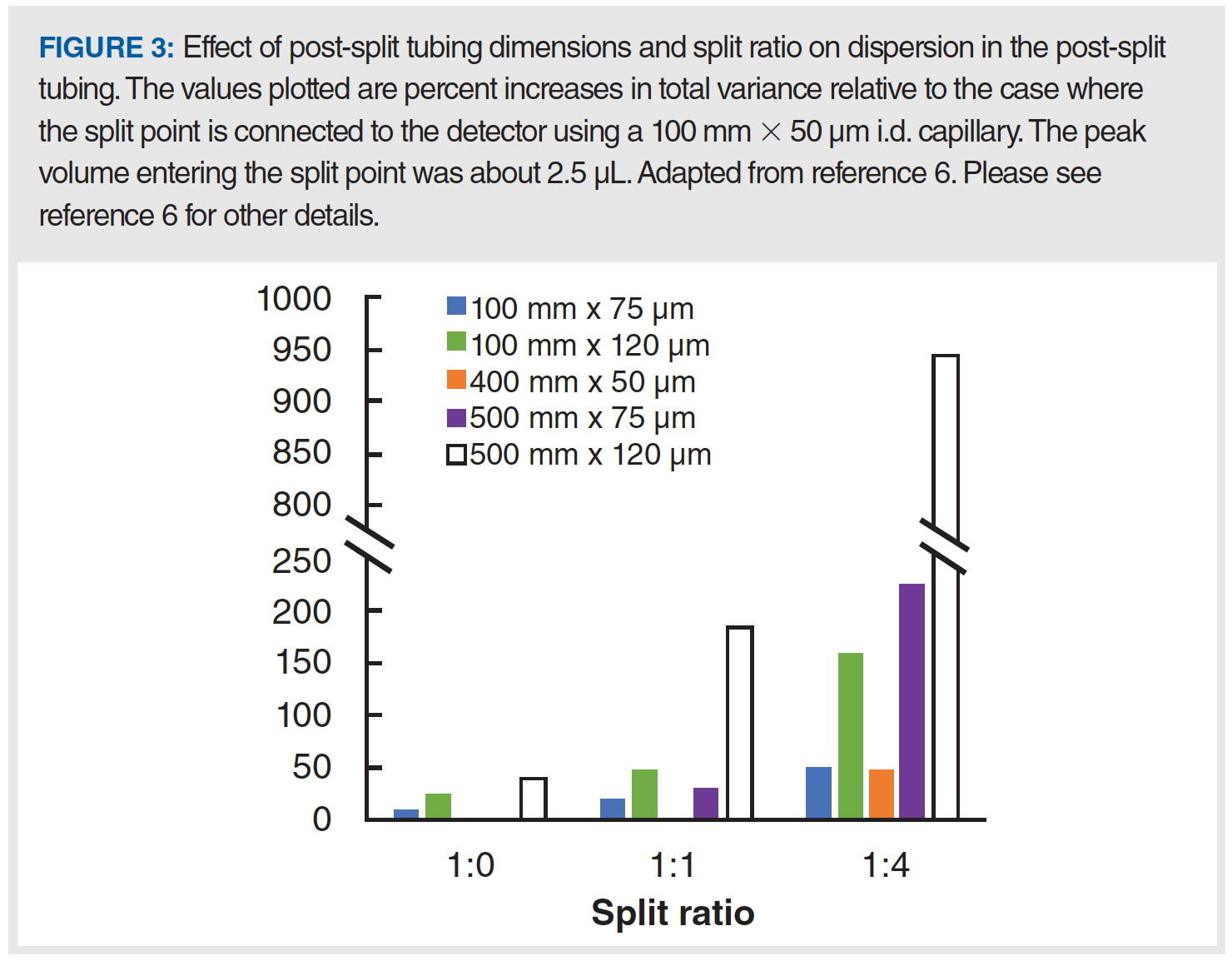
Figure 3 shows a selection of experimental results from our study.
The values plotted are percent increases in the observed variance when using different lengths and diameters of post-split tubing and different split ratios, relative to the case where a short (100 mm), narrow (50 µm i.d.) post‑split tube is used (which contributes very little to the variance under these conditions). When there is no flow split (that is, 1:0 case), the increases in variance because of the different post-split tubes are modest, with just 30% in the worst case of the 500 mm × 120 µm i.d. tube. However, even at a split of 1:1, the variance increases are significant even when using 75 µm i.d. tubes. In the more challenging case of a 1:4 split, even using a 400 mm length of 50 µm i.d. increases the observed variance by about 35%, robbing the analyst of one‑third of the efficiency they expect for their separation. Subsequent comparison of predicted increases in the total observed variance using equations 2 and 3 above with experimental results showed that the predictions are accurate enough to guide method development, with a median error of about 10% of the total variance. This work shows that, when the analyst has a choice, the split point should be located as close as possible to the detector, so that the length of post-split tubing is minimized. Then, once the length has been set, the diameter of the post-split tubing should be decreased as far as possible without significantly increasing the pressure drop across this tube (see next section for more discussion of this point).
Putting It All Together
In this series of instalments on ECD, we have aimed to discuss individual contributions to the total observed variance in some detail. Recent research over the last decade has deepened our understanding of some of these contributions, including the injection step, and the contribution of postcolumn flow splitting. What matters most to the analyst, though, is how all of these contributions taken together impact the quality of their separations. To facilitate use of the theory discussed in these instalments, we have built a web-based calculation tool that allows users to visualize the magnitudes of different contributions to the total observed variance. Figure 4 shows a screenshot of the interface for this free tool. We note that in their free Microsoft Excel-based LC simulator, Guillarme and coworkers also estimate some of these values based on similar input parameters (7).
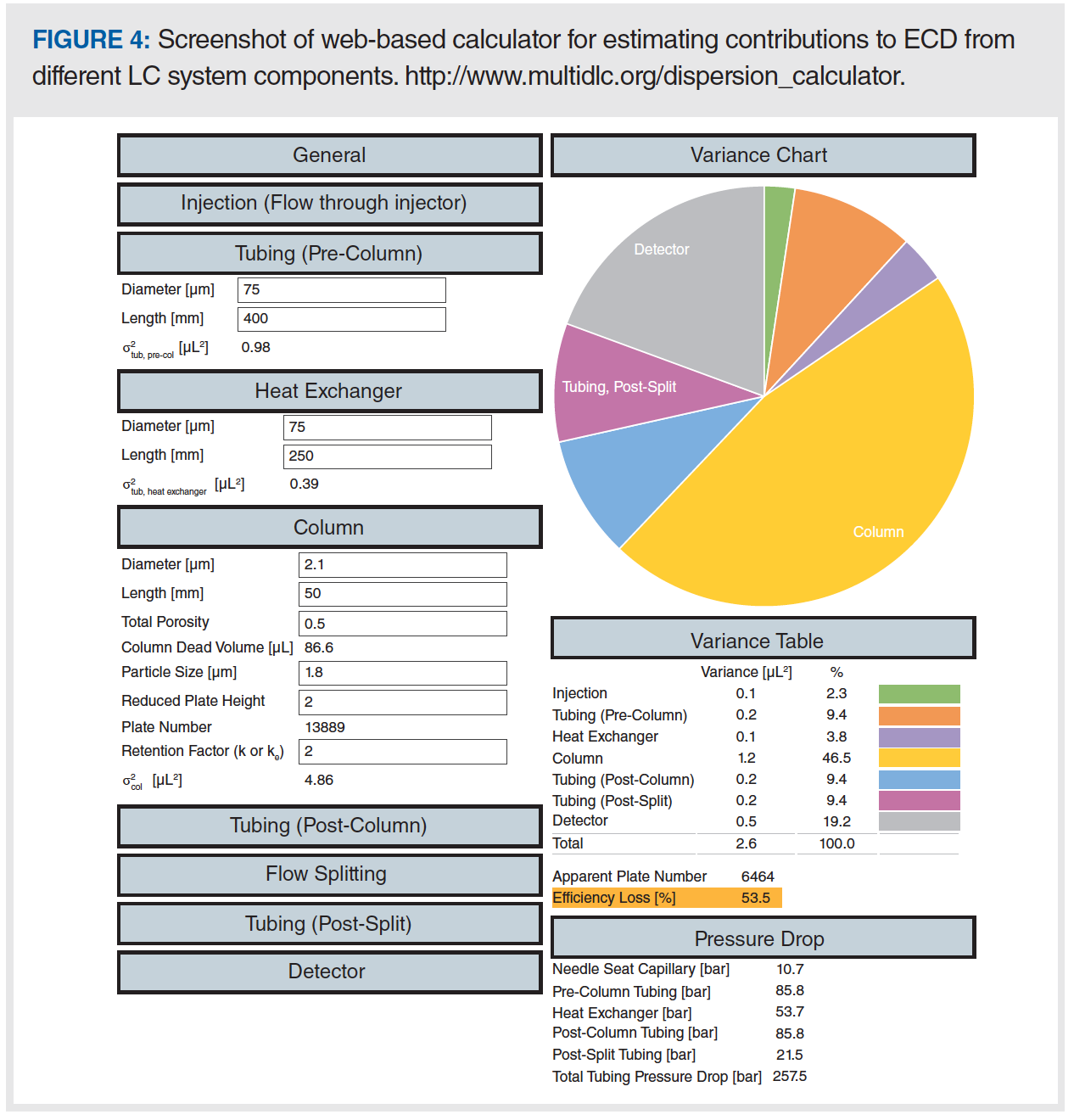
Figure 5 provides examples of how our calculator can be used to guide decisions about different system components (for example, what diameter of postcolumn tubing should be used) during method development. In Case A, we start with a relatively large column packed with 5 µm particles, operated in a system equipped with “standard” injection, detection, and tubing values. In this case, we see that the total observed variance is dominated by the column contribution (~97%), and the pressure drop across the tubing is modest at 36 bar (that is, 10% of the total available pressure drop in a 400 bar system, or about 3% in a 1200 bar system). In the event that one were to think that replacing all of the tubing in the system with 75 µm i.d. capillaries would help squeeze more performance out of the large column used in Case A, Case B is instructive. Here, we see that reducing the injection and detection volumes and reducing the capillary diameters does indeed reduce the total level of ECD, but only by about 2%; also, this comes at the cost of a significantly higher pressure drop across the tubing (236 bar). Indeed, on a 400 bar system, this separation may not even be possible, because there would not be enough pressure left to drive the mobile phase through the column under these conditions.
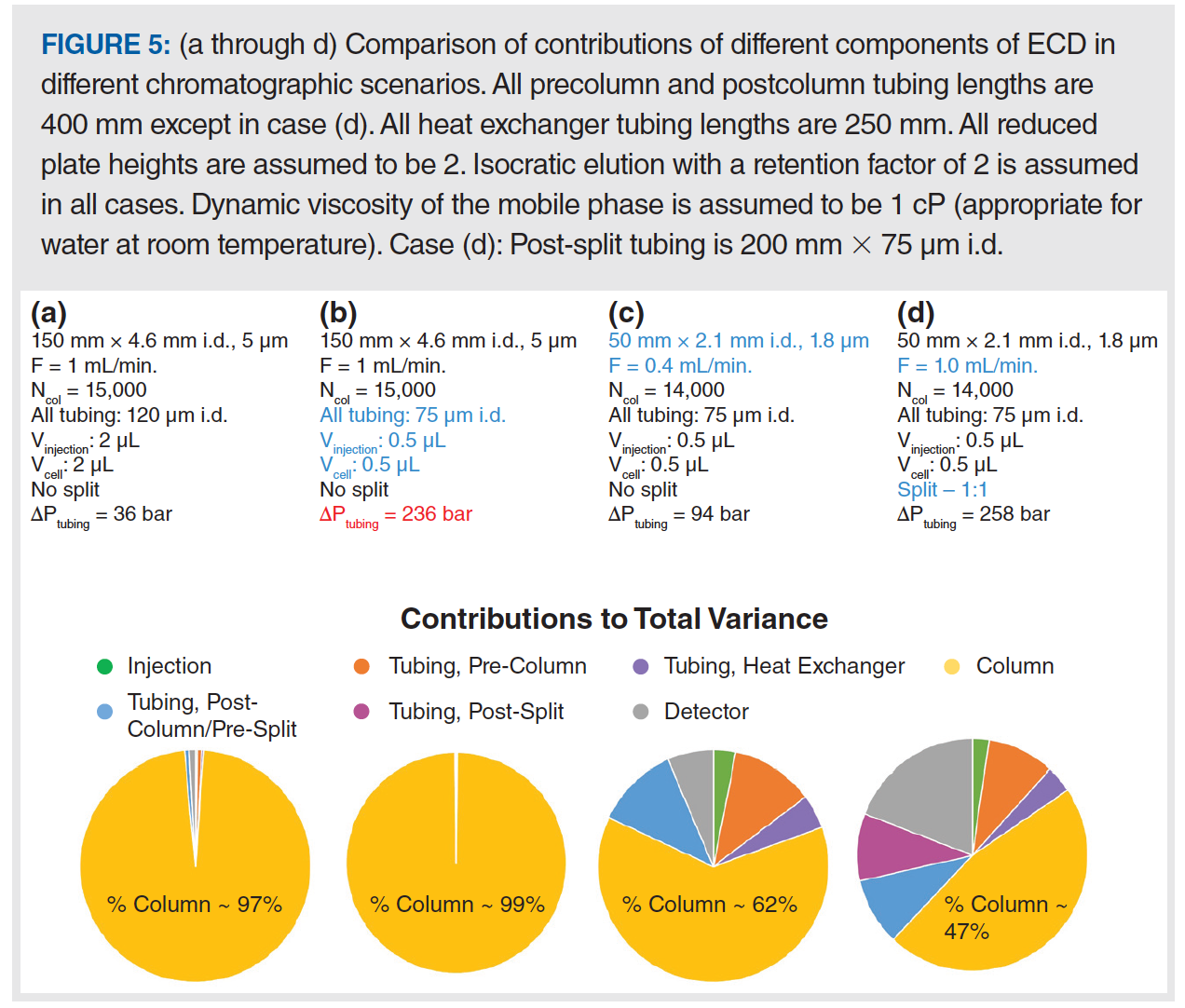
Things become a bit more interesting when we get to Case C. Here, even though we’ve retained “low dispersion” conditions of smaller injection and detection volumes, and smaller 75 µm i.d. capillaries, the contributions of ECD to the total observed variance are about 35%. In other words, the analyst is only realizing about 65% of the expected efficiency of the column because of dispersion in other parts of the system. The pie chart makes it clear that this situation could be improved by reducing the length and/or diameter of the pre- and postcolumn tubing, since these are the major contributors to the ECD in this case.
Finally, in Case D, we illustrate the seriousness of the impact of postcolumn flow splitting when using small columns. This case is the same as Case C, except that: 1) the flow rate through the column is increased slightly; and 2) a 1:1 split has been added with post-split tubing of 200 mm × 75 µm i.d. With these changes, the level of ECD rises to 53% of the observed variance. This is because of the new contribution from the post-split tubing (magenta pie slice), but also to the increased relative contribution from the detector (because the pre-split peak volume is much smaller while the detector volume is unchanged). In this case, the most impactful changes that could be made would be to 1) decrease the detector cell volume (although, this is hard to decrease further without sacrificing signal‑to‑noise ratio [3]); and 2) decrease the lengths or diameters of the post-split tubing, although this must be done very carefully, given that the pressure drop across the tubing is already 258 bar.
Summary
In this instalment of “LC Troubleshooting” we have wrapped up our discussion of details associated with the contributions of specific LC system components to extracolumn dispersion by discussing the impact of elution mode and postcolumn flow splitting. More importantly, we have demonstrated the use of a free web-based calculator that can be used to estimate the magnitudes of contributions to ECD from different system components, and shown how these estimates can be used to guide decisions during method development about which system components to use and which can be modified for maximal performance improvement. We hope that this series of instalments helps to deepen readers’ understanding of the contributions of specific system components to the total level of ECD, and ultimately avoid surprising apparent efficiency losses because of mismatches between column and LC system characteristics that have nothing to do with the performance of the column per se.
Erratum
In Part 3 of this series (3), equation 4 was incorrect. The correct version of this equation is given in equation 4 here.
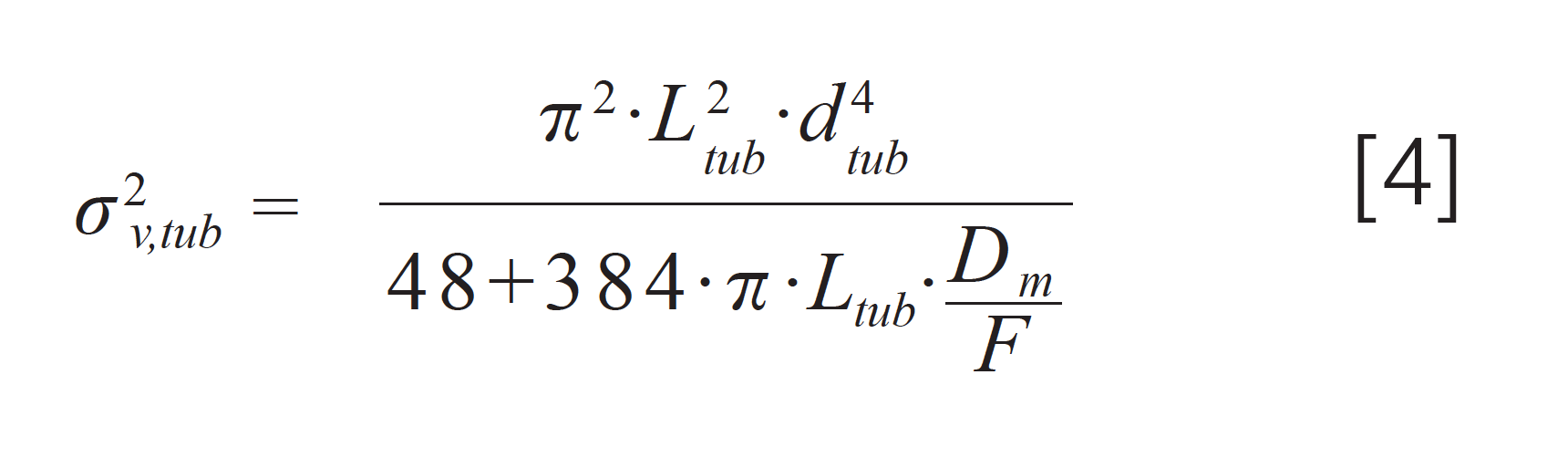
This has been corrected in the website version of Part 3 of this series.
References
- D.R. Stoll and K. Broeckhoven, LCGC Europe 34(5), 181–188 (2021).
- D.R. Stoll and K. Broeckhoven, LCGC Europe 34(6), 232–237 (2021).
- D.R. Stoll and K. Broeckhoven, LCGC Europe 34(7), 277–280 (2021).
- D.R. Stoll, R.W. Sajulga, B.N. Voigt, E.J. Larson, L.N. Jeong, and S.C. Rutan, J. Chromatogr. A 1523, 162–172 (2017). https://doi.org/10.1016/j.chroma.2017.07.041
