The Perfect Method: Part 3: Adjusting Retention

John W. Dolan, LC Resources, Walnut Creek, California, USA.

This is the third installment in a series on method development for liquid chromatography (LC). The focus of the series is on developing new reversed-phase methods in a manner that makes for more reliable methods, while at the same time identifying key areas where problems can occur. In the first section,¹ we looked at goal setting and the second considered the selection of starting conditions.² This month's installment of "LC Troubleshooting" will focus on selection of mobile phase conditions that will give reasonable retention of our sample compounds.

Last month, we concluded that a good starting place for most methods was to use a 150 mm × 4.6 mm, 5 μm particle column or a 100 mm × 4.6 mm, 3 μm column for most sample types. This configuration gives enough theoretical plates (N ≈ 10000 for real samples) to separate most sample types and can be run at 1–2 mL/min for fast method development runs. A mobile phase of low-pH buffer (for example, 25 mM phosphate at pH 2.5) blended with acetonitrile, or optionally methanol, was the mobile phase of choice for UV detection unless you have information to suggest otherwise. For LC–mass spectrometry (MS) applications, a 50 × 2.1 mm, 3 μm particle column operated at 0.2–0.5 mL/min is typical, and 0.1% formic acid is used instead of phosphate buffer. The column temperature is controlled, generally at 30 °C or 35 °C as a starting point.

Our Guide

We'll be using Equation 1 as our guide through the method development process.

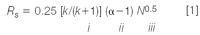
where R_s is the resolution, k is the retention factor, α is the separation factor and N is the column plate number. Recall that the retention factor (sometimes called the capacity factor, k') is

where t_R is the retention time and t₀ is the column dead time (sometimes abbreviated t_m). The column dead time is the retention of an unretained sample component, usually determined by the upslope of the "garbage" or "solvent" peak at the beginning of the chromatogram. We are only concerned about retention (part i of Equation 1) this month. In future instalments, we'll consider parts ii and iii.

Selecting a Target k-Value

To get the "best" chromatography, we strive for 2 < k < 10, but this is often not possible, so 1 < k < 20 is generally acceptable. When k is in one of these ranges, we'll usually get the best separation, but this is not guaranteed. One of the important reasons we would like k > 2 is that resolution is less susceptible to small fluctuations in mobile phase concentration. This is illustrated in Figure 1 and Table 1.

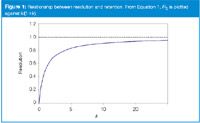
Figure 1

In Figure 1, the influence of retention (term i, Equation 1) is plotted against resolution. If k is infinity, term i approaches 1.0, so this is shown as the maximum possible resolution by the dashed line in Figure 1. I like to think of the influence of k on R_s in three ways.

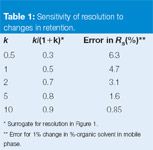
Table 1: Sensitivity of resolution to changes in retention.

First, let's look at getting the maximum power or leverage out of k as a variable to obtain resolution. If 2 < k < 10, we have achieved 70–90% of the possible resolution by adjusting k (see Figure 1 and column 2 of Table 1). This is a pretty good return on our investment in this variable. Increased retention to k ≈ 20 will gain only an additional 5% in resolution, but at a cost of twice the run time and result in broader peaks — not a good trade-off in my opinion. Whereas, if k ≈ 1, we're only at 50% of the maximum resolution, so we are not taking full advantage of this variable. For k < 1, resolution drops off rapidly. Thus, we can see that the 2 < k < 10 or 1 < k < 20 guidelines make sense from the standpoint of taking advantage of the power of k to achieve resolution.

Second, we can consider the susceptibility of a method to small errors in mobile phase composition. For example, if we use a 1% error in mobile phase organic for comparison, we can see that larger k-values are less susceptible to changes in resolution for small changes in percent organic (see Figure 1 and column 3 of Table 1). That is, when compared to the error at k ≈ 10 (0.85%), k ≈ 2 has about three times the error and k ≈ 0.5 is more than seven times the error, with a 6.3% change in resolution for a 1% change in organic solvent. So we can see that methods that generate small k-values will be more susceptible to changes in resolution when small changes in mobile phase composition are made, either as a result of normal variation or as a result of an instrument or operator error.

Finally, real samples almost always generate a large peak at t₀, often called the solvent front or garbage peak, because of unretained materials in the sample. In LC–MS, although a peak at t₀ is usually absent, a general region of ion suppression exists near t₀. In both instances, quantification of analyte peaks can be compromised because of unretained compounds in most samples.

All of these influences support the goal of having 2 < k < 10 for our samples, or if this is not possible, 1 < k < 20. One last way to look at these recommendations is to consider them in light of potential method problems. I have a friend who claims that if every problem LC method were adjusted so that k for the first peak was at least 1, 50% of the problems would go away. I think this is a bit of an oversimplification, but the basic premise is valid. We tend to want to make our method run times short, so peaks get pushed up into the k < 1 region, where there will be more problems with method variation and more likelihood of interference with unretained materials.

What About Run Time?

There is no denying that for most applications, shorter run times are desirable. This is some of the motivation for the current emphasis on sub-2 μm particle columns operated at pressures greater than 6000 psi (400 bar). However, in any application it seems like we will have to trade run time for an increase in k-values. That is, if we have to increase k to get it within the 2 < k < 10 target range, the run will be longer. Contrary to popular opinion, this is not necessarily the situation. Consider the instance in which the current method gives k = 0.5 for the first peak and we adjust the conditions so that k = 2 for the first peak. For a 150 mm × 4.6 mm column operated at 1 mL/min, t₀ ≈ 1.5 min, so we can rearrange Equation 2 to solve for t_R and figure out the retention time in both instances. For k = 0.5, t_R = 2.6 min and for k = 2, t_R = 4.5 min, so the run time nearly doubles. However, if we are willing to increase the flow-rate, we can gain back some or all of this time. For example, most of us run conventional methods with pressures in the 2000–2500 psi region, yet the upper pressure limit for most traditional LC systems is 6000 psi. You can see that doubling the flow-rate will reduce the retention time proportionally, but according to Equation 2, a change in flow-rate has no effect on the retention factor, because both t_R and t₀ change in proportion to flow-rate. Yes, doubling the flow-rate will reduce the column plate number and, thus, resolution, at least in theory. But from a practical standpoint, most methods will not have a noticeable reduction in resolution by a doubling of the flow-rate for columns packed with 3 or 5 μm columns. For example, my calculations for a 150 mm × 4.6 mm column packed with 5 μm particles show that a peak pair with k ≈ 2 and R_s = 1.7 will degrade to R_s = 1.6 when the flow is changed from 1 to 2 mL/min. And this is with a well behaved system — most of our methods are not as sensitive to a two-fold change in flow-rate. So for this example, we have a win-win situation — k is increased to give better chromatography and fewer method problems, yet retention time does not increase. Of course, this assumes that the peak spacing does not degrade with a change in k, which might or might not be true, as we will see in next month's discussion.

Getting k Right

Ok, now we have a target range for k and justification for it, how do we achieve the desired result? One time-honored approach is to start with a strong mobile phase and decrease the mobile phase strength in steps until the desired retention is observed. For example, make a run at 100% acetonitrile, 90%, 80% and so forth. Then when you are close to the desired result, make small changes to fine-tune the separation. This technique works well, and when I worked in an application laboratory for one of the instrument companies, it was the standard procedure.

There is a simpler way. If we make a plot of log(k) versus percent organic (%B) in the mobile phase, we will see a graph similar to that of Figure 2. One of the most striking observations about this graph is that it is linear, so it can be described as:

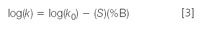
where k₀ is the (extrapolated) value of k at 0% B (100% water or buffer) and S is the slope of the plot. Armed with this relationship, we need only two experimental points to make the plot, not a whole series of 10% steps. This means that once we have made two experimental runs, such as 70% and 50% B in this instance, we can predict the k-value of our sample compound under any other mobile phase concentration. For this example, it is trivial to determine that k = 1 at 81% B and k = 20 at 48% B, so I should first look within the 48–81% B region for the best k-values, and hopefully the best separation.

As we'll see in next month's "LC Troubleshooting," plots similar to Figure 2 for samples of similar molecular weight will have similar, but not necessarily identical, slopes, or S-values. So even without making experimental plots, we can make a generalization of The Rule of Three, which states that a 10% change in mobile phase organic concentration will change k by a factor of about three. This is not a hard-and-fast rule — it can be 2.5 or 4 for some compounds, and applies for compounds of molecular weights less than ≈ 1000 Da, but it gives us a nice guideline. For example, in the earlier instance of a change in k from 0.5 to 2, without any experiments I can guess that the change will require a reduction in mobile phase organic solvent concentration of 10–15%.

Figure 2

Conclusions

We've seen that, from a method development standpoint, it is desirable to adjust retention for that 1 < k < 20, or even better 2 < k < 10. This gives us sample retention times that will give more robust methods in terms of sensitivity to small changes in mobile phase composition. From a troubleshooting standpoint, we can understand that when k < 1 for most methods, besides excessive sensitivity to mobile phase composition, there is more likelihood of quantification problems because of interferences at t₀.

The regular behaviour of retention and mobile phase organic concentration in reversed-phase LC, as illustrated in Figure 2, gives us a tool to use to find experimental conditions more quickly that will give us retention in the desired range. You might have noticed, however, that a change in %B to change k often results in a change in relative retention, or peak spacing, as well. This can be a problem that can create problems when we try to increase k to move peaks away from t₀, but, as we'll see in next month's instalment of "LC Troubleshooting," we can use such changes in selectivity to our advantage so as to finetune a separation with very little extra work.

"LC Troubleshooting" Editor John W. Dolan is vice-president of LC Resources, Walnut Creek, California, USA and a member of LCGC Europe's editorial advisory board. Direct correspondence about this column to "LC Troubleshooting", LCGC Europe, Advanstar House, Park West, Sealand Road, Chester CH1 4RN, UK.

Readers can also direct questions to the Chromatography Forum at www.chromforum.com

References

1. J.W. Dolan, LCGC Eur., 20(9), 438–443 (2007).

2. J.W. Dolan, LCGC Eur., 20(10), 504-509 (2007).