Moore’s Law in Liquid Chromatography: An Overview of 50 Years of (U)HPLC

Image Credit: stock.adobe.com/majcot

This article quantifies the progress in speed and efficiency that has been made in the area of liquid chromatography (LC) over the past 50 years. After a decade of groundbreaking advances in the 1970s, the progress in chromatographic performance over the ensuing four decades (1980–now) follows Moore’s law relatively closely. This is characteristic of technological fields that are of an evolutionary nature (that is, driven by the need for better performance).

Last year (2019), we celebrated the 50th anniversary of the famous 1969 Zlatkis meeting, generally recognized as the symposium where most of the founding fathers of high performance liquid chromatography (HPLC), such as Huber, Giddings, R.P.W. Scott, Horvath, Snyder, Kirkland, Halasz, and Pretorius, gathered for the first time to discuss their work in the area of liquid chromatography (LC) (1–2). And this year, we celebrate the 50th anniversary of Csaba Horvath’s 1970 Pittcon lecture, where he first coined the acronym “HPLC”. Since these pioneering days, the progress in speed and efficiency has been impressive. This progress was realized by improvements in packing procedure, particle size and particle size distribution, available instrument pressure, instrument design and, in the past decade, also by the (re-)introduction of core–shell particles.

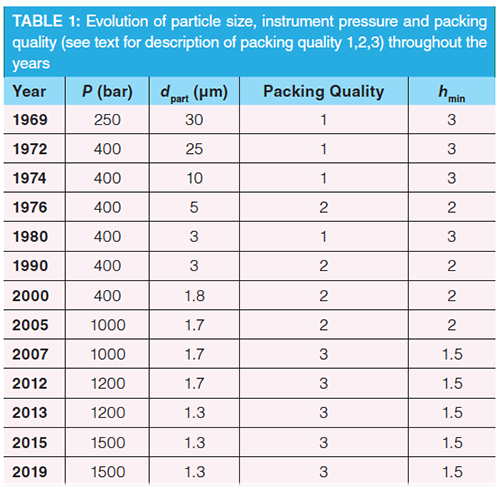
Table 1 provides an overview of some of the milestone dates contributing to this progress. For some, a clear moment in time can be identified, while for some others only a rough indication can be given. The packing quality is an example of the latter. Early references usually assume h_min = 3 or more (3), while in 1980 there is already clear mention of a h_min = 2-plate height (4), albeit obtained with relatively large particles while the state-of-the-art 3-μm particles available at that time still produced a value of h = 2.5–3 (5). By the end of the 1990s, h_min = 2 had become the “gold standard” for the best possible packed columns, regardless of the particle size (6). The (re-)introduction of core–shell particles on the other hand, producing plate heights as low as h_min = 1.5 or even less, can clearly be situated and dated in the year 2007 (7). And, in recent years, it has also been shown that the evolution of the packing quality for fully-porous particle columns does not have to stop at h_min = 2. When carefully engineering the particle size distribution, minimal plate heights well below 2 (around h_min = 1.7-1.8) are also within reach for fully-porous particle columns (8).

Also the history of the successive introduction of ever-smaller particle sizes is not easy to reconstruct in detail. A clear landmark was the commercial introduction of 10-μm particles in 1974. Soon after came the first mentions of the use of 5-μm particles in academic papers (9), while 3-μm particle separations started to appear in literature in the beginning of the 1980s (5,10). The next breakthrough came with the introduction of sub-2-μm porous particles in the beginning of the 00’s, which became commercially-available in 2003 (1). Leaving aside non‑porous particles, the smallest commercially-available particle is currently a 1.3-μm particle, introduced in 2013 (11).

Easier to date are the breakthroughs in (commercially-available) instrument pressure. The first main event was the introduction of the first commercial pump enabling separations at pressures of 6000 psi or 400 bar in 1972 (12). The introduction of ultrahigh-pressure liquid chromatography (UHPLC) can be considered the second landmark event, introducing the era of UHPLC with instrument pressures of 1000 bar and beyond (13). Nowadays, the maximally available inlet pressure on a commercial instrument is 1500 bar (14).

In the present contribution, it is attempted to quantify the progress in terms of speed and efficiency resulting from the (r)evolutions listed in Table 1. More specifically, it is investigated whether the progress in HPLC follows Moore’s law. This empirical law was proposed in 1965 by G.E. Moore, one of Intel’s founders, to describe and predict the long-term progress made in the micro-electronics industry (15,16). This law states that clock speed and memory storage capacity are roughly doubling every two years. Over the years, Moore’s law has also been reformulated in a more general way to apply it to other fields, expressing that the logarithm of the performance varies linearly with time:

Log(performance) = a*#years+b            [1]

with a and b given constants. In other words, in fields obeying Moore’s law, progress occurs exponentially. Since its initial introduction, many fields outside electronics (for example, gene sequencing, internet connectivity in bits/s) have been found to follow this general version of Moore’s law, at least when they are of an evolutionary nature (that is, driven by the need for better performance).

Rather than trying to make a list of the successive breakthroughs in speed and efficiency limits reported in literature, which is virtually an impossible task (not least because speed and efficiency studies seldom occur under comparable conditions), the present contribution follows a more theoretical approach, calculating the achievable speed and efficiency for each of the entries in Table 1, using the well-established kinetic performance expressions governing LC. This approach is outlined in the next section, which can be skipped if one is only interested in the results.

Theory

In a first approximation, the packing quality of packed bed columns can always be represented by Knox’ semi-empirical reduced plate height equation (6):

h = A.ν^1/3+B/ν +C.ν          [2]

Here, the following parameter-values were used: A = 1.2, B = 2.5, C = 0.15 for packing quality 1; A = 0.7, B = 2.5, C = 0.075 for packing quality 2, and A = 0.4, B = 2.5, C = 0.05 for packing quality 3 (= core–shell columns). All three packing qualities are assumed to have the same B-value. This reflects the fact that the longitudinal diffusion is in principle independent of the packing quality. With the aforementioned values, the minimal reduced plate heights respectively correspond to h_min = 3.0 (packing quality 1), h_min = 2.0 (packing quality 2) and h_min = 1.5 (packing quality 3). The u₀-based flow resistance was put at ϕ₀ = 800 for packing quality 1 and 2, while it was put at ϕ₀ = 600 for packing quality 3 (= core–shell columns).

In the present study, the progress in performance has been calculated for two different cases: fixed analysis time and fixed efficiency N. All calculations were carried out in MS-Excel.

The calculations for the fixed analysis time proceeded as follows. Using the identity L = u0.t0, Kozeny’s pressure drop law can be written as:

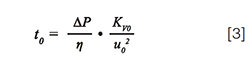
Isolating u₀ in equation 3 and subsequently linking u₀ to its dimensionless equivalent ν (via ν = u₀.dp/D_mol), equation 2 can be rewritten as:

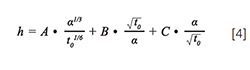
wherein α is a constant that can be calculated as α = [ΔP/(η.ϕ)]^0.5.d_p²/D_mol.

Considering now a given total analysis time t_anal = t₀(1+k), and subsequently fixing the retention factor of the last eluting compound (k=9 throughout present study), the value of t₀ is fixed as well. With also ΔP, η, ϕ, d_p and D_mol chosen or known, we can calculate α for every entry in Table 1 and subsequently use equation 4 to calculate h. From this value, it is then straightforward to obtain the value of N via the well-established:

N = L.H = u0 ¥ t0 ¥ h ¥ dp                             [5]

The same set of equations can be used if the required efficiency N is fixed (fixed N-calculation). However, in this case the MS-Excel solver needs to be used to determine the value of t₀ for which the desired N satisfies the set of equations 3–5.

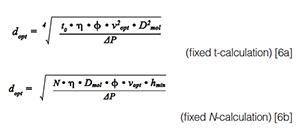
In both cases, the particle size that has been used was either the smallest particle size available at that time, or, if another, larger particle size is more optimal for the desired time or N, the latter value was taken. These optimal particle sizes were calculated using either one of the below well-established equations ([6a] and [6b]) (17):

Results

Calculated using the approach described in the previous Section, the data in Figure 1 show how the number of theoretical plates N that can be achieved in a t_anal = 30 min run has been steadily increasing over the years, going from N = 1000 in 1970, to N = 140 000 today, at least if using a system with the best possible column, optimized particle size and column length, and making full use of the available commercial instrument pressure (250 bar in 1970, 1500 bar nowadays). Clearly, the largest leaps in performance were made between 1970 and 1980, during which period the minimal particle size was reduced from around 50 to 25 μm down to 5 μm and the first 400 bar instruments became available. Drawing the best fit Moore’s law trend line over the 1970–1980 period (line not shown), a value of a = 0.1491 (R² = 0.8254) is found for equation 1, corresponding to an increase in N of about 41% per year. If progress had continued at the same rate, our systems and columns would now be producing over 30 000 000 000 theoretical plates in a 30 min run (t₀-time = 3 min). Obviously, this did not happen, as the progress made in the next two decades (1980–2000) occurred at a much slower pace. In this period, technological evolution was mainly limited to the elaboration of better packing procedures and a relatively modest reduction of the particle size, with 3 μm particles being the standard at the end of the 1990s. On the other hand, a big leap in performance was again made mid-2000, with the introduction of UHPLC technology and the (re-)introduction of the core–shell particles. After these groundbreaking events, progress has considerably slowed down again in the past decade, where the most important advances result from a further increase of the available pressure from 1000 to 1500 bar, as well as from a modest decrease of the minimal available particle size. This has recently been brought down to 1.3 μm (11).

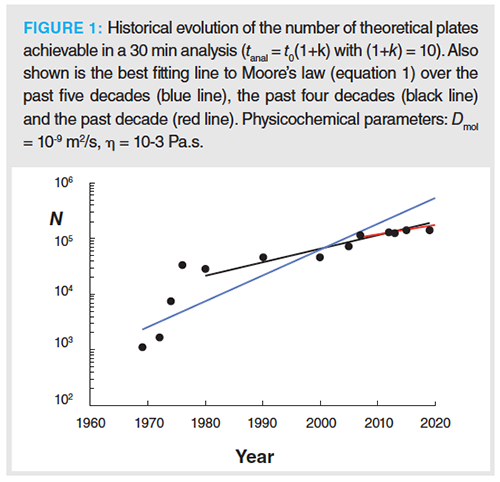
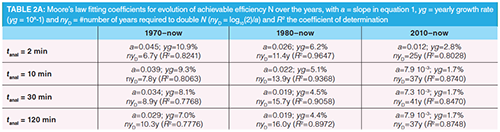
Given the clear difference in progress rates before and after 1980, Moore’s law produces a weak fit to the data when applied over the entire 50-year span (black trend line,
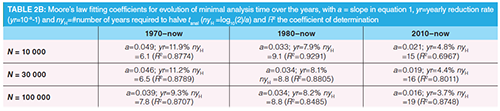
Figure 1), resulting in a coefficient of determination of only R² = 0.777 (see 30 min entry in Table 2[a], second column). A much better coefficient of determination is obtained when only considering the last 40-year period (1980–now, blue trend line, Figure 1). With a value of R² = 0.9058, progress over this period can be said to closely follow Moore’s law, with an annual growth rate of 4.5% per year (a = 0.0192, see Table 2[a]). Measured over the last decade, the progress in N corresponds to a rather meager value of a = 0.0073 or, equivalently, an increase of about 1.7% per year (see red trend line in Figure 1, and 30 min entry in Table 2[a], last column).

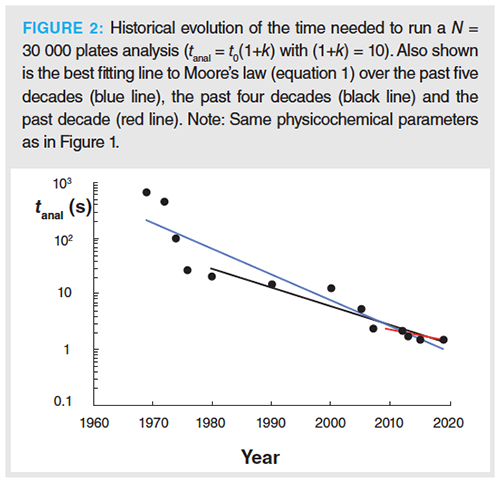
Fully similar observations can be made for the evolution of the time needed to produce 30 000 theoretical plates (Figure 2). While this time was brought down from 670 mins in 1970 to 1.5 mins today, over the last 50 years, the largest part of this impressive progress was realized between 1970 and 1980. If the increase in speed would have continued at the same rate as was realized in that period, we would now be doing 30 000 plate separations in less than 1 ms. Clearly this is not the case, as progress has slowed down considerably in the ensuing 40 years. Given the large difference in progress rate between the 1970s and the following decades, the fit with Moore’s law is again relatively poor over the entire five-decade period, while there is a better fit with Moore’s law over the last four-decade period. Over the last 40 years, the annual speed gain was at 8.14% per year (a = -0.034, see Table 2[a]). The fact that the rate with which the analysis time reduces is roughly twice that of the increase in efficiency, N can be readily derived from Knox’ separation impedance expression (with E = H²/K_v, with K_v = hydraulic permeability) (17):

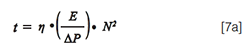
Considering that the improvements in particle and packing quality and in available instrument pressure are combined in the (E/ΔP)-factor, equation 7 readily shows that any reduction of this (E/ΔP)-factor leads to a linearly-proportional reduction of the time required to produce a given N. On the other hand, rewriting equation 7a as:

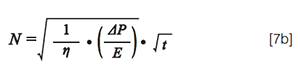
shows that a reduction of the (E/ΔP)-factor only leads to a square-root improvement of N when t is fixed. In logarithmic units, the difference between a linear power and a square root power corresponds to a factor of 2 difference in slope, hence explaining the approximate factor of 2 difference between the a-values in Figures 1 and 2.

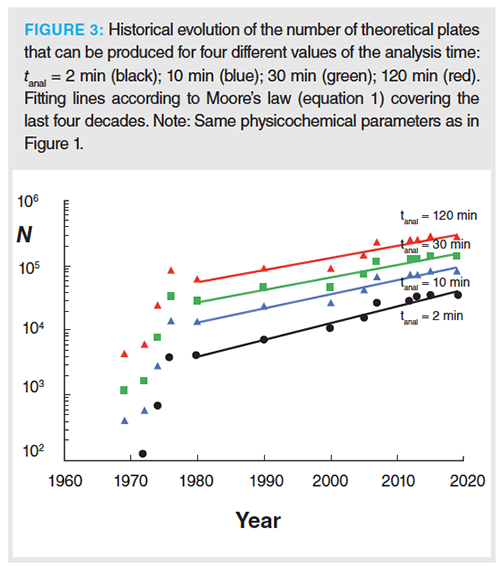
Repeating the exercise of the time-driven analysis for other values of the total analysis time (Figure 3), the pattern already observed in Figure 1 for the 30 min analysis time case is, apart from some small differences, also observed for the other considered times. The main observable difference between the different t_anal-cases is that the progress made in the last four decades is slightly steeper for the shortest separations. This is also reflected in the a-factors and annual growth rates represented in the third column of Table 2(a), which consistently decrease with increasing t_anal. This trend can be understood by considering that high-speed separations benefit most from the availability of small particles, while the high efficiency separations (large tanal) have larger optimal particle sizes, and these larger sizes were already available earlier on.

Table 2(a) also shows the period giving the best, most consistent fit with Moore’s law is always the 1980–now period, for all four considered tanal-values, all producing R²-values around or well above 0.9 over this last four-decade period.

The R²-values also show a consistent trend, with R² monotonously decreasing with increasing tanal (cf. R²-entries in third column of Table 2[a]). This is mainly due to the fact that the leap made around 2005–2007 with the introduction of the UHPLC instruments had a higher impact on the high efficiency separations than on the high speed separations. The latter require such short columns that the 400 bar instruments that were available at that time already allowed us to partly exploit the kinetic advantages of the sub-2-μm particles introduced in the beginning of the 2000s, while the high efficiency separations really needed the +1000 bar pressures of the UHPLC instrumentation.

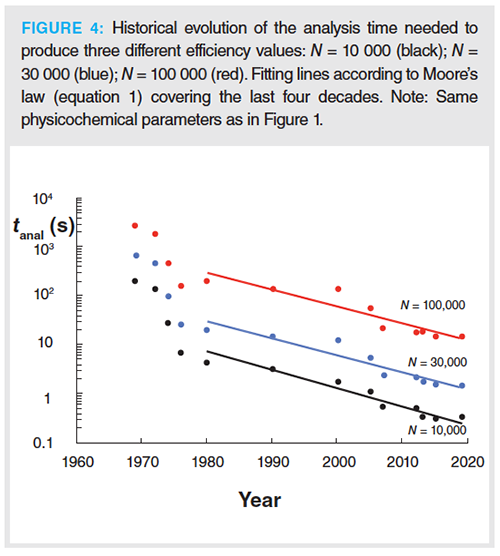
The observations that can be made from Figure 4 (= evolution of tanal for a fixed N over the past decades) are very similar to those made for the evolution of N for a given t_anal shown in Figure 3, and will hence not be repeated here. The average yearly reduction rates (cf. third column of Table 2[b]) are roughly double those of the increase in N (8% vs 4.5%), in agreement with the discussion of equations 7(a–b). An exception to this rule needs to be made however for the high speed/low efficiency separations, where the yearly progress rates lie closer to each other. The latter can be explained by the fact that these separations are typically conducted in the C-term dominated regime, while the above discussion of equations 7(a–b) is strictly speaking only valid around the optimum velocity. Overall, the fitting quality of Moore’s law is slightly less good than for the evolution of N in Figure 3 (average R²-value = 0.88 versus 0.92). This can be explained by the fact that the breakthrough in performance made around 2005–2007 by the introduction of UHPLC instruments and core–shell particles has a stronger impact on the separation speed than on the achievable efficiency (t~E/ΔP versus N~ΔP/E)1/2, see equations 7[a–b]), hence inducing a stronger local deviation from the linear trend.

Conclusions

The present analysis shows that, after a decade of groundbreaking progress in the 1970s, the progress in chromatographic performance over the ensuing four decades (1980–now) nicely follows Moore’s law, representing and predicting a long-term exponential growth. The average yearly increase in achievable theoretical plates N for a fixed total analysis time is of the order of 4.5–6.2%, while the reduction of the required time needed to conduct a separation with given N is of the order of 7.9–8.2%. Whereas these percentages may not seem much at first sight, they correspond to an improvement with a factor 6–11 (increase in N), resp. 20–23 (gain in speed) when compounded over the last 40 years. These are truly impressive achievements.

However, progress occurs with shocks, with periods of sudden acceleration alternated with longer periods where technology advances only slowly. These outbursts of progress are always linked to groundbreaking events, such as the introduction of 400 bar instruments in the 1970s or the introduction of the UHPLC instruments and the (re-)introduction of core–shell particles in the 2000s.

The occurrence of such groundbreaking events or paradigm shifts is well-known to lead to deviations from Moore’s law, which assumes a gradual improvement of an existing approach. Hence the relatively low coefficient of determination R² over the five-decade and one-decade periods considered in Table 2. Since we are currently also living in an era with very low progress, it is clear the field is in need of another paradigm shift. The shape this paradigm shift will assume is difficult to predict (pillar array [18] or 3D-printed columns; core–shell particles with strictly radially-oriented pores? [19]; improved versions of the silica monolith?), but we should be confident that new technologies and new material possibilities will bring the HPLC area new surges of progress, as happened in the past.

References

1. R.E. Majors, LCGC North America33(11), 10–19, 27 (2005).
2. C.E. Arnaud, C&E News 94(24), 28–33 (2016).
3. I. Halasz, H. Schmidt, and P. Vogtel, J. Chromatogr. 126, 19–33 (1976).
4. P. Kucera, J. Chromatogr.198, 93–109 (1980).
5. E. Katz and R.P.W. Scott, J. Chromatogr. 253, 159–178 (1982).
6. J.H. Knox, J. Chromatogr. A.831, 3–15 (1999).
7. F. Gritti, A. Cavazzini, N. Marchetti, and G. Guiochon, J. Chromatogr. A.1157, 289–303 (2007).
8. O.H. Ismail, M. Catani, L. Pasti, A. Cavazzini, A. Ciogli, C. Villani, D. Kotoni, F. Gasparrini, and D.S. Bell, J. Chromatogr. A.1454, 86–92 (2016).
9. I. Halasz, R.Endele, and J. Asshauer, J. Chromatogr. 112, 37–60 (1975).
10. J.L. Di Cesare, M.W. Dong, and J.G. Atwood, J. Chromatogr.217, 369–386 (1981).
11. C. Sanchez, G. Friedlander, S. Fekete, J. Anspach, D. Guillarme, M. Chitty, and T. Farkas, J. Chromatogr. A.1311, 90–97 (2013).
12. Pat McDonald, Chemical Heritage (Waters Corporation) (2008).
13. Davy Guillarme, Elia Grata, Gaetan Glauser, Jean-LucWolfender, Jean-Luc Veuthey, and Serge Rudaz, J. Chromatogr A.1216, 3232–3243 (2009).
14. J. De Vos, M. De Pra, G. Desmet, R. Swart, T. Edge, F. Steiner, and S. Eeltink, J. Chromatogr. A. 1409, 138–14 (2015).
15. G.E. Moore, Electronics38, 114–117 (1965).
16. R.R. Schaller, IEEE Spectrum34, 52–59 (1997).
17. J.H. Knox and M. Saleem, J. Chromatogr. Sci. 7, 614–622 (1969).
18. W. De Malsche, J. Op De Beeck, S. De Bruyne, H. Gardeniers, and G. Desmet, Anal. Chem.84, 1214–1219 (2012).
19. T.C. Wei, A. Mack, W. Chen, J. Liu, M. Dittmann, X. Wang, and W.E. Barber, J. Chromatogr. A. 1440, 55–65 (2016).

Gert Desmet heads the Department of Chemical Engineering at the Vrije Universiteit Brussel, Belgium. His research mainly focuses on the miniaturization and automation of separation methods, as well as on the investigation and the modelling of flow effects in chromatographic systems. He is an Associate Editor for the journal “Analytical Chemistry” and holder of an ERC Advanced Grant.