Gradient Elution, Part II: Equivalent Separations

Is it possible to get the same separation under isocratic and gradient conditions?

In last month's "LC Troubleshooting" (1), we began our series of discussions on gradient elution. We saw that liquid chromatography (LC) separations under isocratic and gradient conditions had some of the same properties when operating conditions are changed. For example, when run times are made longer, resolution tends to improve, peaks broaden, and peak height drops. Longer run times are obtained in reversed-phase LC by reducing the concentration of the organic solvent (%B) in isocratic separations or increasing the gradient time (reducing the gradient steepness) with gradients. In this installment, we'll see how to compare gradient and isocratic separations under "equivalent" conditions.

When Isocratic Won't Work

In Figure 1a, we see a chromatogram for the isocratic separation of 15 compounds at 60% B. Several deficiencies are seen. The peaks early in the chromatogram are narrow and tall, but the first two are poorly resolved. At the end of the chromatogram, the peaks are well separated, but they are broadened excessively. The run takes nearly 30 min. If we try to improve the separation at the beginning of the chromatogram, we would reduce the %B in the mobile phase. This would increase the retention of the early peaks, and in general is expected to improve the resolution. However, the peaks at the end of the run would broaden more and move to even longer retention times — neither of which is desirable. Alternatively, we could improve the separation at the end of the chromatogram by increasing the %B, which would reduce the retention times, close up some of the gaps between the peaks, and sharpen the peaks. But the higher %B would compress the chromatogram at the beginning, making it even worse.

Samples such as in Figure 1a are a good example of the general elution problem. In such cases, it is difficult or impossible to get a satisfactory separation for all the peaks under a single isocratic condition. We can improve the beginning or end of the chromatogram, but not both at the same time. The reason for this is that the polarity range of the sample is too large. Recall that under the most desirable conditions, we'd like the retention factor, k, to be 2 < k < 10, but if 1 < k < 20 can be obtained, we often can find acceptable separation conditions. In the present case, 0.9 < k < 34, so the k range (34/0.9 ≈ 38) is approximately twice the maximum we would like (20/1 = 20). When samples such as this are encountered, a gradient is likely to give a better separation.

What About a Gradient?

When the sample of Figure 1a is run under gradient conditions, we get the separation of Figure 1b. We can quickly see that the separation is improved. The resolution between peaks is increased at the beginning of the run and the excess time between peaks at the end of the run in Figure 1a is reduced. Thus, the peaks are spread out more evenly across the chromatogram. Also, note that the peak widths throughout the run are approximately the same. Narrower peaks at the end of the run translate into taller peaks, so detection is improved in this part of the chromatogram. Finally, for the present sample, the run time is reduced by a factor of four. All these improvements make the gradient a better choice for this sample. (Gradients, however, are not always better, as we saw in last month's "LC Troubleshooting" [1] in which an isocratic separation was a better choice.)

Figure 1: Simulated chromatograms for the separation of a 15-component sample on a 150 mm × 4.6 mm column operated at 2 mL/min: (a) isocratic separation at 60% B, (b) gradient separation of 50–100% in 5 min, and (c) isocratic separation of subsets of 15-component sample such that k ≈ 3 for each group. Peak identity and %B are noted on chromatograms.

Comparing Isocratic and Gradient Separation

Next, let's look at isocratic and gradient separation under so-called equivalent conditions. By this we mean mobile-phase conditions under which the retention and peak properties are roughly the same with both isocratic and gradient runs.

It should be obvious that if we consider only a single peak, we should be able to find isocratic and gradient conditions that will give approximately the same retention time and peak width. To illustrate this, I've broken the 15-component sample into five subsamples in Figure 1c. In each case, I've adjusted the isocratic %B so that k ≈ 3 is obtained for the peaks. For example, at 49% B in Figure 1c, peak 1 has a retention time, t_R, of 2.9 min and for peak 2, t_R = 3.2 min. Under these conditions, the column dead time, t₀, is 0.75 min. We can calculate the k value for each peak from k = (t_R– t₀)/t₀. So k₁ = (2.9 – 0.75)/0.75 = 2.87 and k₂ = 3.26. The average k value at 49% B is 3.07 ≈ 3. In a similar manner, we find that 61% B gives k ≈ 3 for peaks 3–7, 72% for peaks 8–9, 80% for peaks 10–12, and 88% for peaks 13–15. In each case, the retention times of the peaks in each group are approximately the same, so the peak widths are approximately the same, as we'd expect under isocratic conditions.

Next, compare the isocratic peaks in Figure 1c with the appropriate section of the gradient in Figure 1b. Notice that in both separation modes all the peaks are approximately the same width. Also, the peak spacing between adjacent peak pairs is nearly the same in both cases. You can mentally connect the isocratic chromatograms of Figure 1c and get a separation that is very close to that of Figure 1b.

Because we see the same peak behavior in Figures 1b and 1c, we say that these are equivalent conditions. The only catch is that we have to have several different isocratic conditions to match a single gradient. But this gives us another way to visualize what is happening during a gradient. If we could program the LC system to run a series of isocratic steps that would maintain the separations of Figure 1c, we would start at 49% B until peak 2 was eluted, then step to 61% until peak 7 comes out, and so forth. Of course steps like this won't give us exactly the same separation, because the peaks of each segment are influenced by the conditions of the prior segment, but it serves as a useful mental model. After all, a gradient can be thought of as a series of isocratic steps where the step size is infinitely small. Under such conditions we get the results of Figure 1b.

With the isocratic separations of Figure 1c, all the peaks traveled through the column with k ≈ 3. The retention factor, k, is a useful tool for developing isocratic separations and describing isocratic retention. When equivalent gradient conditions are used, Figures 1b and 1c suggest that the peak characteristics are approximately the same, so the retention factors also should be similar. To avoid confusion between isocratic and gradient retention factors, the gradient retention factor is abbreviated as k*, which can be thought of as the average k value throughout the separation.

Band Migration in Gradient Elution

Another way to think about how gradient elution works is shown in Figure 2. In Figure 2b, we see a chromatogram overlaid with the gradient program (dashed line). For discussion purposes, let's assume that the gradient is a linear gradient of 5–100% B over 20 min. In Figure 2a, the left-hand y-axis tracks the band migration as it moves through the column (in the direction of the arrow on the axis); the band position is shown by the solid curved lines. The isocratic k value at any instant during the run is plotted on the right-hand y-axis; the instantaneous k value is shown as the curved dashed lines.

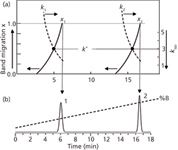
Figure 2: Peak migration of peaks 1 and 2 during gradient elution. (a) Plot of peak position in the column, x1 and x2 shown by solid curves and left-hand axis; plot of instantaneous isocratic k value, kiso, at any time during the separation shown by dashed curves and right-hand axis; solid dots representing kiso at the midpoint of the column, x = 0.5, equivalent to k*; (b) gradient program, dashed line; chromatogram for peaks 1 and 2 when they reach the end of the column, x = 1.0. Adapted from Figure 9.3 of reference 2.

We'll consider two bands, 1 and 2, as they travel through the column. Under the initial conditions (5% B), peak 1 is very strongly retained, so it appears to sit at the head of the column (migration position of 0), and the isocratic k value is very high (dashed line off-scale). As the gradient progresses, stronger solvent runs through the column, and eventually the solvent is strong enough to move the band off the head of the column, and it begins to migrate through the column. Meanwhile, the k value drops (downward arrow on the right-hand y-axis). With each increase of %B, the solvent is stronger, which means that the band travels faster, accelerating through the column. Meanwhile, the stronger solvent results in a smaller instantaneous isocratic k value, so k continues to drop. This acceleration of the sample band and drop in k continue until the band reaches the end of the column (migration = 1.0), and a peak appears in the chromatogram.

In a similar manner, band 2 moves through the column. But because 2 is less polar than 1, it stays at the head of the column longer before a strong enough solvent arrives to begin carrying it through the column. However, its migration pattern through the column (the curvature of the migration plot) is very similar to band 1, but offset to higher %B values. The value of k₂ also drops during the run in the same manner as k₁.

If we ignore the time the sample bands sit on the head of the column doing nothing, and only consider the time that they actually migrate through the column, you can see that this migration time is about the same for both bands. In isocratic separation, two bands that take the same amount of time to go through the column will have the same retention times, and thus the same peak widths. This is another way of understanding why all peaks in a gradient run are approximately the same width — they take the same amount of time to migrate through the column.

The gradient k value, k*, can be thought of as the equivalent of the isocratic k value when a band has migrated halfway through the column. For band 1, the band reaches the midpoint of the column (x₁ = 0.5, black dot in Figure 2a) at 5 min. Tracing this k value to the right shows that k_iso = 3 for peak 1; thus k* = 3. Similarly, band 2 reaches the midpoint of the column at ~15 min, which also corresponds to k_iso = 3 = k*. Both bands reach the midpoint of the column with the same k value, so k* is the same for both peaks. And as we noted above, if the effective migration time of each peak is about the same, we would expect the same isocratic k, so it isn't surprising that k* is approximately the same for all peaks in a gradient run.

Figure 2 also helps us understand one oversimplified description of gradient elution. This states that sample compounds sit at the top of the column until a strong enough solvent comes along to wash them off, then they travel quickly through the column. This is a bit simplified, and doesn't give the column much credit for the separation, but it gives us a basic understanding of how bands behave under gradient conditions.

Summary

Let's review what we've covered here. We saw that if the range of isocratic k values is too large, a single isocratic separation will be very difficult without sacrificing peak height and run time. In such cases, where the ratio of k values for the first and last peaks exceeds ~20, a gradient usually will give better results. Figure 1c was used to demonstrate that if the number of peaks in a sample is limited, we usually can get ideal isocratic chromatography (2 < k < 10) by choosing the right %B. And by breaking up a complex sample into small sections, we can obtain similar k values for all peaks in the sample, albeit under different conditions.

When the series of isocratic separations with k ≈ 3 for all peaks (Figure 1c) was compared with the gradient separation of the same sample (Figure 1b), the results were surprisingly similar. Further dividing the chromatogram into an infinite number of isocratic steps is equivalent to running a linear gradient, in this case obtaining k* ≈ 3 for all peaks.

Figure 2 helped to illustrate that k* is equivalent to the isocratic k value at the point a band has moved halfway through the column. It also showed that all peaks tend to migrate through the column in a very similar manner, with the primary difference being how long they sit at the head of the column before significant band migration occurs.

Although not discussed here, Figure 2 also can be used to determine the influence on retention of changing the initial or final %B in a gradient, as well as the gradient steepness (or gradient time) and the shape of the gradient.

References

(1) J.W. Dolan, LCGC North Am. 31(3), 204–209 (2013).

(2) L.R. Snyder, J.J. Kirkland, and J.W. Dolan, Introduction to Modern Liquid Chromatography, 3rd ed. (Wiley, Hoboken, New Jersey, 2010).

John W. Dolan "LC Troubleshooting" Editor John Dolan has been writing "LC Troubleshooting" for LCGC for more than 25 years. One of the industry's most respected professionals, John is currently the Vice President of and a principal instructor for LC Resources, Walnut Creek, California. He is also a member of LCGC's editorial advisory board. Direct correspondence about this column via e-mail to John.Dolan@LCResources.com

John W. Dolan