New Horizons in Reversed-Phase Chromatography Selectivity

For decades, reversed-phase (RP) chromatography has dominated HPLC applications. Almost as soon as bonded reversed phases became available in the early 1970s, this mode surged ahead as the most popular. Through the years, the technique has become more efficient, columns more stable, and new types of phases beyond the traditional C8 and C18 give different selectivity that is required for more difficult separations. Here, we focus on the characterization of reversed-phase columns with particular emphasis on the hydrophobic-subtraction model. A well-attended Pittcon 2010 session brought together many experts to update our knowledge in this area and help liquid chromatographers make more educated decisions on phase selection and usage.

In a recent HPLC column survey,¹ over 95% of all respondents used reversed-phase (RP) chromatography in their daily work. The popularity of this technique is undoubtedly due to its versatility. Reversed-phase chromatography can separate nonpolar, polar, ionizable and ionic compounds, sometimes at the same time. For mobile phases, reversed-phase chromatography uses water (often buffered) and a water-miscible organic solvent; both are relatively plentiful in most parts of the world in HPLC grade purity.

At Pittcon 2010, Dr Lloyd Snyder of LC Resources (Walnut Creek, California, USA) and Professor Peter Carr of the University of Minnesota (Minneapolis, Minnesota, USA) organized a full-day symposium on RP column selectivity with an emphasis on the hydrophobic-subtraction model.^2–5 The two sessions brought together academic and industrial people who are expanding on and using this model to tackle the subject of column selectivity in this most popular mode.

Brief History of RP Chromatography Chemistries

The technique of high performance liquid chromatography (HPLC) had its beginnings in the late 1960s. In the beginning of HPLC, there was no reversed-phase chromatography as we know it today.

The original 1950 publication titled Separation of C₁₂–C₁₈ Fatty Acids by Reversed-Phase Partition Chromatography by Howard and Martin,⁶ which outlined the basics of liquid–liquid chromatography with a nonpolar stationary phase and a polar mobile phase, lay dormant for a couple of decades while workers in the field pursued other chromatographic approaches such as paper, adsorption and thin-layer chromatography (TLC). The problem for liquid–liquid partitioning reversed-phase chromatography in those early days was first homogeneously coating, then keeping the coated nonpolar stationary phase on the surface of the polar base material while an aqueous–organic solvent mixture was running over its surface.

This liquid–liquid partition mechanism was never very successful in TLC and also proved unsuccessful in the early days of LC. However, the development of a hydrocarbon polymer-coated Zipax (called Zipax HCP) material by Kirkland and DeStefano⁷ gave a more stable surface than the coated liquid phases. However, as admitted by Kirkland coworker Reed Williams with the Dupont Liquid Chromatography business at the time, "With the liquid- and polymer-coated packings, one dared not change the mobile phase very much for fear of stripping the stationary phase from the packing."⁸ The early brush-type bonded silicate ester phases (Si–O–CH₂–R)⁹ suffered from some of the same problems not because the phase would mechanically strip off of the packing, but because the chemical bond could be easily hydrolysed and was thermally unstable.

The answer to the dilemma came in the successful development of chemically bonded silicone (siloxane) phases (Si–O–Si–C) based upon the work of Aue and Hastings.¹⁰ The first commercial, chemically bonded phase was Permaphase, developed by Kirkland and coworkers.11 Rather than being coated, Permaphase was a chemically bonded polymeric phase applied to the pellicular support Zipax. Compared with liquid–liquid partitioning phases and polymer-coated phases, with this polymeric-bonded phase, column life was much longer, stronger mobile phases could be used and gradient elution could help solve the 'general elution problem'. However, due to slow solute diffusion in the polymeric layer, column efficiency was not as great as anticipated. The solution, now in popular use today, was the development of the nonpolar, monomeric bonded siloxane phase.¹² Here a monochloro- or monoalkyoxy-silane containing a strongly hydrophobic hydrocarbon moiety, such as octadecylsilane (ODS, C18), was reacted with the surface silanol to produce a stable, higher efficiency bonded phase. Monomeric phases are, by far, the most widely used reversed-phase packing today and the basis for most theoretical and practical models of retention, efficiency and selectivity.

Gas chromatography (GC) had been plagued by the proliferation of many stationary phases. Unlike GC, with only the stationary phase and temperature as major variables, liquid chromatographers initially felt that the ability to manipulate the mobile phase would cut down the number of stationary phases to only a few. In the preface of the 1974 book on chemically bonded phases, editor Eli Grushka, then at the Chemistry Department of the State University of New York at Buffalo, stated, "We do not wish to encourage proliferation of many bonded phases, each suited for a particular separation."¹³ He went on to state, "Further work should be directed, perhaps, at a better understanding of bonded phase characteristics, thus developing a relatively small number of systems that could be utilized for multiseparation purposes." Nevertheless, to date, there are well over 1000 reversed-phase columns alone¹⁴ and the list keeps growing. Thus, a number of workers^15–20 have tried to come up with a simple scheme to understand selectivity in reversed-phase chromatography. The hydrophobic-subtraction model^2,4 appears to be gaining favour as an approach that can be fairly universal in its application. The remainder of this instalment of "Column Watch" will be devoted to the papers presented at Pittcon 2010 on this model as well as other approaches to reversed-phase chromatography selectivity.

The Hydrophobic-Subtraction (H-S) Model of Reversed-Phase Column Selectivity

Many different procedures have been used to describe the selectivity of reversed-phase columns (for example, references 15–20). The H-S model differs from all of these in being derived experimentally, without initial assumptions about the various interactions between solutes and the column, yet results in a quantitative (and presumably fundamental) description of each column–solute interaction. Several thousand measurements of retention factors k for 150 different solutes and about 100 type-B alkylsilica columns (C₁–C₃₀) have been predicted by the equation

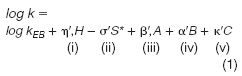
with an accuracy of ±1–2%. Here, k is the value of kEB for a reference solute (ethylbenzene), and terms i–v describe contributions to retention from five solute-column interactions: (i) hydrophobic, (ii) steric interaction, (iii) hydrogen-bonding of basic solutes to (acidic) silanols, (iv) hydrogen bonding of acidic solutes to basic groups within the stationary phase and (v) cation-exchange between a cationic solute and ionized silanols –SiO^–. The Greek letters (η', σ' and so forth) refer to properties of the solute, while capital letters describe properties of the column that can be measured by means of Equation 1: column hydrophobicity H, steric resistance to penetration by the solute S*, hydrogen-bond acidity A and basicity B, and cation-exchange capacity C (a measure of silanol 'acidity' or ionization). These five parameters can be easily measured²¹ and used to characterize different columns in terms of selectivity. Except for C, which varies with mobile-phase pH, each parameter can be assumed constant for different mobile phases or temperatures. Two additional interactions are present for cyano (π–π, dipole–dipole) and phenyl (π–π) columns, but are of limited significance for most samples.

Two columns can be compared in selectivity by means of a function F_s:

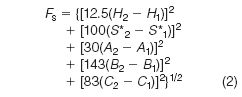
where H₁ and H₂ refer to values of H for columns 1 and 2, and similarly for S*, A, B and C. Values of F_s can be regarded as the distance between columns 1 and 2 in a five-dimensional space defined by the five column parameters. Two columns with a small value of F_s will be similar in terms of selectivity, while large values of F_s indicate two columns of quite different selectivity. The empirical factors (12.5, 100, etc.) recognize differences in the relative contributions of H, S* and so on to sample resolution.

Henry agreed with Neue that large groups of solutes should be studied by LC–MS to survey a wide range in phase properties. He also made a plea for manufacturers to provide more information on the chemistry of their phases.

How Can the H-S Model Be Used?

Because of the fundamental nature of the H-S model, it seems suited to a wide range of applications of column selectivity, some of which were reported for the first time at Pittcon 2010:

• Selection of similar columns, as back ups for routine assays.^22,23

• Selection of dissimilar columns, for a change in separation during method development, the development of orthogonal separations to ensure that no 'new' peaks are present and 2D separation.^23,24

• Avoidance of columns that are more likely to result in tailing peaks (usually for bases, but sometimes for acids).²⁵

• Development of new stationary phases of unique selectivity.²⁶

• Prediction of column 'dewetting'.²⁷

• Improved control of column manufacture.^28–30

• A better understanding of stationary phase degradation during routine use.²⁵

• 'Slow' column equilibration for ionized solutes.³¹

• Deeper insights into the nature of reversed-phase retention and column selectivity, as well as the factors that determine column selectivity.^32,33

• Quantitative predictions of separation for different columns, with the possibility of choosing a specific, 'best' column for a given sample.³⁴

Let's take a closer look of some of these applications using the H-S model.

Column Equivalency

Reversed-phase HPLC is widely used in the pharmaceutical industry. Most pharmaceutical methods require a back up column. The H-S model can be used to find a column that is 'equivalent' based upon the testing parameters mentioned previously. M. Marques of the United States Pharmacopeia (USP) reviewed both the history of column classification by the USP and two current procedures for the measurement of column selectivity.³⁵ The USP approach, developed in cooperation with the National Institute of Standards and Technology, is based upon the retention times of five test compounds: uracil, toluene, ethylbenzene, quinizarin and amitriptyline. The H-S model comprises the second USP procedure, referred to by USP as the Product Quality Research Institute procedure (the PQRI provided support for the evaluation of the H-S model). The USP website (http://www.usp.org/USPNF/columns.html) allows the user to compare the selectivity of two columns by either procedure. There are 120 C18 columns in the USP database and 480 reversed-phase columns of all kinds in the PQRI database (which continues to be updated). Two similar, widely promoted methods for comparing column selectivity were also noted: the Advanced Chemistry Development (ACD, Toronto, Ontario, Canada) ACD Labs Column Selector and Katholieke Universiteit (Leuven, Belgium) Column Classification System. Over the past 18 months, the column equivalency section of the USP website has been visited 1400–1900 times per month. It had been hoped that users would offer comments on which of the two USP procedures they preferred, but so far, little feedback from the public has been received.

A presentation by A. Schellinger of Abbott Laboratories (North Chicago, Illinois, USA)³⁶ was based entirely upon the hydrophobic-subtraction model. The thrust of the work was to compare the selectivities of various groups of phases chosen based upon their H-S parameters, their F_s values (Equation 2) and their positions in the H-S triangle of Zhang and Carr²⁸ for some 25 drugs containing multiple basic sites.³⁷ The point was to test the concept "Will phases chosen to be similar based upon the H-S model actually be similar based upon their selectivities as established by a set of basic drugs?" Four groupings of reversed phases were chosen:

• Very similar type-B alkyl phases.

• Phenyl phases.

• Phases that are internally similar but quite different from the preceding phases.

• Phases chosen to be different from one another and all other phases tested.

By and large there was a good correlation between the standard error (S.E.) values of the drug-based comparison of phases to the S.E.-based upon a comparison using test compounds from the 16 solutes used by Snyder and Dolan² to establish the phase parameters. The chief deviation was a Nova Pak cyano phase (Waters, Milford, Massachusetts, USA). Schellinger also discussed the use of gradient elution to compare phases. The standard conditions used to measure the H-S model parameters are isocratic (50:50 acetonitrile–water phosphate buffers at pH 2.8 or 7.0). It was shown that gradient conditions give very similar column classification if one bases selectivity on the scatter in plots of retention time vs retention time not log k versus log k as is done in the original isocratic Snyder–Dolan method.²

Column Development and Manufacturing

The use of the H-S model can be quite helpful in column and bonded phase development from the commercial side. F. Dorman (Restek, Bellefonte, Pennsylvania, USA)²⁹ reviewed the use of the H-S model in his laboratory for the purpose of comparing different columns in terms of selectivity. In one study, measurements of the column-selectivity parameters H, S* and so forth were made for column packings for which either the bonding process or starting silica was changed. As expected, a change of silica was found to have the largest effect, affecting mainly values of silanol acidity C at low pH. A comparison of selectivity among various Restek columns were investigated next, with a sample of the 16 test-compounds that are used to measure values of H, S* and so forth. Each of the five sample-column interactions of Equation 1 are exhibited strongly by two or more of these test-compounds, so resulting chromatograms for each column provide a visible display of changes in each interaction (as well as corresponding changes in H, S*, etc.). Thus, the Restek IBD column was found to have greater hydrogen-bond basicity B, so that phenols and acidic solutes were retained most strongly. Similarly, the Aq-C18 and PFP-propyl columns had the most acidic silanols (largest C) and preferentially retained protonated basic solutes. Finally, Equation 2 was used to rank different columns in terms of selectivity.

In his use of the H-S model at Grace Davison Discovery Sciences (Carnforth, Lancashire, UK), I. Chappell³⁰ began by describing how column selectivity (as measured by values of H, S* and so forth) changes with bonding level (ligand concentration) for extended-polar-selectivity phases and concluded that this enables the design of phases with selectivity matched to the application. He then considered the manufacture of packings for large-scale preparative separations, where a selectivity similar to that obtained with more costly spherical packings is required for these low-cost irregular silicas. The question he considered was "How do we measure and control selectivity on transfer between silica types?" By varying the bonding level, it was possible to adjust for differences in the base silica, resulting in the same column-selectivity parameters for different bonded phases. His final conclusion was "The Snyder/Dolan/Carr approach to measuring reversed-phase selectivity is a powerful tool in media design and control."

Investigation of pH and Buffer Concentration Effects on Ionization of Reversed-Phase Columns

Retention in reversed-phase HPLC is dominated by hydrophobic interactions (H, Equation 1), but selectivity can be influenced strongly by other column properties (S*, A, B, C). A presentation by J. Dolan (LC Resources, Walnut Creek, California, USA)³³ examined ionic interactions, concentrating on the C-term of the H-S model, which describes the cation-exchange capacity of a column at different pH values. As pH is increased for type-B columns, the retention of ionized bases is increasingly due to ion exchange. However, at pH < 5, ion pairing appears to play a more important role in the retention of bases, especially for columns with C-2.8 < 0.1. The presentation also looked at the effect of endcapping on reducing cation-exchange capacity of type-B columns. There is a clear correlation with the reduction of C-7.0 (cation-exchange capacity at high pH) with column endcapping (Figure 1). However, no change in cation-exchange capacity at low pH (C-2.8) is observed when the column is endcapped. It was speculated that this might be due to different types of silanol groups being responsible for ion-exchange at high and low pH, and that these groups might respond differently to the endcapping reaction.

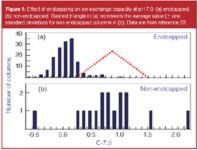
Figure 1

Selection and Classification of Dissimilar Reversed-Phase Columns

In certain applications, it is useful to have a way to select and compare dissimilar reversed phases. For example, in comprehensive two-dimensional liquid chromatography (LC×LC), the two columns should be as orthogonal as possible with different retention mechanisms to achieve the highest peak capacity.

Quality by design (QbD) is a strategy used in the pharmaceutical industry to improve the quality of analytical processes. QbD is "a systematic approach to development that begins with predefined objectives and emphasizes product and process understanding and process control, based upon sound science and quality risk management" (ICH Q8 R1). In his talk using a QbD prespective, L. Wrisley of Pfizer (Pearl River, New York, USA)²³ stated that one predefined objective is that an HPLC method should be developed on a column that has an alternate equivalent stationary phase available. A second goal is that an orthogonal method should be available to confirm that all peaks are separated by the primary method. The PQRI column database³⁵ was used as a tool to make these column selections. Several examples were given, in which it was shown that the database could be used both to ensure that an alternate (equivalent) column was available before starting method development (for example, see Figure 2) and that a predicted orthogonal column could be used to help show that the primary method had adequate selectivity. Laboratory experiments were minimized by the use of modelling software (DryLab, a product of Molnar Institute, Berlin, Germany and Design-Expert, a product of QualityCoach.Net, Wooster, Ohio, USA) to predict robustness and which experiments to run to demonstrate robustness.

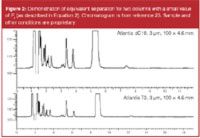
Figure 2

Selectivity Variables in Reversed-Phase Method Development

In reversed-phase method development, the traditional variables (%-organic, gradient time, temperature, pH, organic solvent type, additives) can be modelled easily with retention-modelling software, such as DryLab. In his presentation, I. Molnar (Molnar Institute, Berlin, Germany)³⁴ demonstrated a new version of this software that uses a cubic resolution map to enable the examination of three independent variables (for example, gradient time, temperature, and pH) and their interactions to predict optima and minimize experimental work to show robustness. Also presented was a technique of column selection alluded to in reference 32 where a sample of known or unknown composition is injected on six columns of widely differing selectivity to characterize the η', σ', β', α' and κ' values (Equation 1) for each peak in the sample mixture, as summarized in Figure 3. In this paper, columns were also selected with the aid of the PQRI database.³⁵ Once these sample characteristics are known, a column giving optimal selectivity can be predicted by the database for use in method development. This column-selection technique is preliminary in nature and requires more development to show broad applicability.

Figure 3

Alternative Approaches for Addressing Selectivity in Reversed-Phase Chromatography

Stationary Phase Triangle Scheme: Professor Peter Carr (University of Minnesota, Minneapolis, Minnesota, USA) presented an alternative approach that allowed visualization of stationary phase selectivity.²⁸ He used triangle graphs based upon the well-known Snyder selectivity triangle to display the relative selectivity of some 360 phases thus far studied by the hydrophobic subtraction model.⁴ The Carr method compares selectivity based not upon the absolute value of the phase parameters (H, S* and so forth) as in Equation 2, but rather in accord with the principle of effective selectivity developed by Zhao.⁴⁰ The Carr procedure is based upon the four relative phase parameters (S*/H, A/H, B/H and C/H). To plot three-dimensional data in a two-dimensional graph, the data must be normalized appropriately.²⁶ Because there are four relative phase parameters a full description requires a set of four independent triangles (S-B-C, S-A-C, A-B-C, S-A-B). The major strength of the method is that it allows visualization of all phases simultaneously (Figure 4). Inspection clearly shows that only a small fraction of the total selectivity space is occupied, hence pointing to where new phases would have substantial impact, and not merely serve as "me too" phases. Another advantage of the method is that it allows subsets of phases to be compared. For example, one can readily compare the selectivities of the class of all phenyl phases against all type B C8 silica phases. Finally, it is an easy matter to visually spot those phases that should produce the most extreme changes in selectivity.

Figure 4

Selectivity based upon correlation coefficients: The presentation of U. Neue of Waters (Milford, Massachusetts, USA)⁴¹ differed from all the other talks in the symposium in several regards. Most importantly, a method for comparing and evaluating different contributions (stationary phase, eluent type and pH) to total chromatographic selectivity was developed. The key metric is related to the correlation coefficient (r²). Mathematically r² is the fraction of the variance in the dependent variable (y) due to the independent variable (x). If a plot of log k versus log k on two columns for a common set of probe solutes had no scatter then r² would be precisely 1.000. According to the H-S model, the two phases would have no difference in selectivity. In Neue's work, he makes plots of gradient elution retention time, which is more or less the same as a log–log plot for isocratic elution. He then computes selectivity s as:

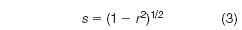
A minor caveat in this approach is that it is only statistically valid if the two sets of retention times are adjusted or normalized to cover the same range, so that the slope of the plots of t_R versus t_R are very close to unity. Neue proposed that if one were to compare two different phases, under two different eluent conditions — for example, gradient elution with methanol vs acetonitrile as modifier and at two different pH values — then:

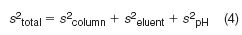
In the simpler case of variations only in phase and eluent but not pH this results in a 'prism' plot that shows the effect of changing the two variables (see Figure 5).

Figure 5

For each variable the s value is obtained by fixing the other properties and determining retention of a common set of solutes. Thus s² eluent would be measured by using the same column and same pH, but on one axis, methanol would be used, and on the other axis, acetonitrile would be used. For this approach to be exactly true, each of the contributions would have to be independent of the others. When these ideas were applied to a very large body of data for many different solutes obtained by LC–MS, Neue concluded that

• The strongest selectivity effects are caused by pH changes (provided the analytes have ionizable functions). This agrees with earlier work by Gilar and associates.⁴²

• Rather strong selectivity differences are observed in a combination of changes of the stationary phases [alkyl versus phenyl versus EPG (embedded polar group)] together with solvent changes (methanol versus acetonitrile).

• The biggest selectivity changes are obtained by combining more than one parameter, such as column type and organic modifier and pH.

Principal component analysis for characterization of stationary phases: M. Euerby of Hichrom (Theale, Berkshire, UK)⁴³ reviewed a different procedure for measuring column selectivity,¹⁹ based upon previous work by Tanaka.¹⁶ Users can access the procedure in a program (ACD Labs Column Selector) at the ACD website (http://www.acdlabs.com). Data for 266 columns are available, with additional columns being added. The column-selectivity characteristics measured by this procedure are similar to five of the six determined by the H-S model: hydophobicity, shape selectivity, hydrogen-bond acidity and the positive charge on the column (silanol capacity) at both low and high pH. These column parameters can be used for many of the applications of the H-S model listed earlier. Euerby also emphasized the use of principal component analysis for the further interpretation of column—selectivity data, especially for an understanding of the effects of different column-sample interactions on the final separation and its benefits for method development. A nice feature of this procedure is that for the vast amounts of data that are generated, one gets a visual output for easier comparisons.

Novel Stationary Phases

R. Henry, a well-known LC expert and consultant, gave a wide ranging discussion of stationary-phase factors and their impact on chromatography selectivity.⁴⁴ A major point of the talk was that the phase chemistry controls selectivity. This was illustrated nicely by comparing the exceptional retention of nitro-aromatic compounds (electron-deficient species thus π-acids) on phenyl phases, which act as π-base phases as compared to alkyl phases. An interesting point was raised that some chromatographic variables (%B, pH, temperature) are continuous and we can predict and adjust them more easily than we can discontinuous variables such as phase type. The impact of mobile phase on phase selectivity was also a major theme of this presentation. It is well known that less methanol than acetonitrile is sorbed by alkyl bonded phases. It was pointed out that acetonitrile can then act to suppress differences in selectivity between phases. Henry agreed with Neue⁴¹ that large groups of solutes should be studied by LC–MS to survey a wide range in phase properties. He also made a plea for manufacturers to provide more information as to the chemistry of their phases.

Conclusion

In years to come, reversed-phase chromatography will continue to dominate HPLC applications. Column technology will continue to evolve rather than revolve. In the selectivity area, even though there have been myriad bonded phases introduced over the decades of reversed-phase chromatography, special phases will continue to be developed to solve niche separation problems. The greater use of the H-S model during the future development of new reversed-phase chromatography columns might lead to a smaller number of more useful columns (i.e., having greater differences in selectivity). With the growing interest in comprehensive LC (for example, LC×LC), orthogonal phases will be required that are compatible with the aqueous phases of reversed-phase chromatography yet provide a different selectivity.

Problems that cannot be solved by reversed-phase chromatography, especially dealing with very polar unretained compounds, might be solved by hydrophilic interaction liquid chromatography, which is experiencing great growth at this time.

"Column Watch" editor, Ronald E. Majors, is a senior scientist at the Columns and Supplies Division, Agilent Technologies, Wilmington, Delaware, USA and is a member of LCGC Europe's editorial advisory board. Direct correspondence about this column should be addressed to "Column Watch", LCGC Europe, Poplar House, Park West, Sealand Road, Chester CH1 4RN, UK or e-mail amatheson@advanstar.com

Peter Carr obtained his BS at the Polytechnic Institute of Brooklyn in 1965 and his PhD in Analytical Chemistry at Pennsylvania State University in 1969. He was assistant and associate professor of Chemistry at the University of Georgia from 1969–1977 and the associate professor at the University of Minnesota from 1977–1981. Between 1981–2010 he was a professor at the University of Minnesota and he has also acted as co-chairman at the International Conference on Column Liquid Chromatography held in Minneapolis in 1994.

Dr Lloyd Snyder is from the University of California at Berkeley where he obtained his BS in 1952 and his PhD in 1954. He has been principal at LC Resources Corp. from 1984–present and has co-authored the Introduction to Modern Liquid Chromatography, 3rd ed. (with J.J. Kirkland, J.W. Dolan).

John W. Dolan is LC Troubleshooting editor in LCGC Europe and has written three books with Lloyd Snyder on various aspects of HPLC and spends much of his time with LC Resources providing practical training for LC users around the world.

References

1. R.E. Majors, LCGC N. Am., 27(11), 956–972 (2009).

2. N.S. Wilson et al., J. Chromatogr. A, 961, 171 (2002).

3. L.R. Snyder and J.W. Dolan, LCGC N. Am., 20(11), 1016–1026 (2002)

4. L.R. Snyder, J.W. Dolan and P.W. Carr, J. Chromatogr. A, 1060, 77 (2004).

5. L.R. Snyder and J.W. Dolan, LCGC N. Am., 22(12), 1146–1152 (2004)

6. G.A. Howard and A.J.P. Martin, Biochem. J., 46, 532–538 (1950).

7. J.J. Kirkland and J.J. DeStefano, J. Chromatog. Sci., 8, 309 (1970).

8. R.C. Williams in "Bonded Stationary Phases in Chromatography", E. Grushka, ed. (Ann Arbor Science, Ann Arbor, Michigan, 1974), p. 29.

9. I. Halasz and I. Sebastian, Angew. Chem. Interat. Ed., 6, 453 (1969).

10. W.A. Aue and C.R. Hastings, J. Chromatogr., 42, 319 (1969).

11. J.J. Kirkland, Anal. Chem., 43(12), 36A–48A (1971).

12. R.E. Majors and M.J. Hopper, Abstract No. 42 Analytical Division, 160th National Meeting of the American Chemical Society, Chicago, Illinois, USA. September, 1970.

13. E. Grushka in Bonded Stationary Phases in Chromatography, E. Grushka, Ed., (Ann Arbor Science, Ann Arbor, Michigan, 1974), Preface page vi.

14. R.E. Majors, Recent Developments in LC Column Technology, LCGC N. Am. Supplement, 28(4S), 8–17 (2010).

15. H.A. Claessens, Trends Anal. Chem., 20, 563–583 (2001).

16. N. Tanaka, K. Sakagami and M. Araki, J. Chromatogr., 199, 327–337 (1980).

17. K. Kimata et al., J. Chromatogr. Sci., 27, 721 (1989).

18. U.D. Neue, J. Sep. Sci., 30, 1611 (2007).

19. M.R. Euerby and P. Petersson, J. Chromatogr. A, 994, 13 (2003).

20. D. Visky et al., J. Chromatogr. A, 1012, 11 (2003).

21. L.R. Snyder et al., J. Chromatogr. A, 1057, 49 (2004).

22. J.W. Dolan et al., J. Chromatogr. A, 1057, 59 (2004).

23. L. Wrisley, Pittcon 2010, Orlando, Florida, USA, paper no. 2540–5, 4 March 2010.

24. J.W. Dolan and L.R. Snyder, J. Chromatogr. A, 1216, 3467 (2009).

25. D.M. Marchand, L.R. Snyder, and J.W. Dolan, J. Chromatogr. A, 1191, 2 (2008).

26. Y. Zhang and P.W. Carr, J. Chromatogr. A, 1216, 6685 (2009).

27. L.R. Snyder, J.J. Kirkland and J.W. Dolan, Introduction to Modern Liquid Chromatography, 3rd ed. (Wiley–Interscience, Hoboken, New Jersey, 2009), p. 237

28. P.W. Carr, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–1, 4 March 2010.

29. F. Dormann, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–5, 4 March 2010.

30. I. Chappell, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–6, 4 March 2010.

31. D.M. Marchand and L.R. Snyder, J. Chromatogr. A, 1209, 104 (2008).

32. L.R. Snyder, Pittcon 2010, Orlando, Florida, USA, paper no. 2540–1, 4 March 2010.

33. J.R. Dolan, Pittcon 2010, Orlando, Florida, USA, paper no. 2540–4, 4 March 2010.

34. I. Molnar, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–8, 4 March 2010.

35. M. Marques, Pittcon 2010, Orlando, Florida, USA, paper no. 2540–3, 4 March 2010.

36. A.P. Schellinger, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–3, 4 March 2010.

37. W. Fan et al, J. Chromatogr. A, 1216(38), 6587–6599 (2009).

38. L.R. Snyder, J. Chrom. Sci., 16, 223 (1978).

39. N.S. Wilson et al., J. Chromatogr. A, 961, 217–236 (2004).

40. J. Zhao and P.W. Carr, Anal. Chem., 70, 3619–3628 (1998).

41. U.D. Neue et al, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–2, 4 March 2010.

42. M. Gilar et al, Anal. Chem., 77, 6426–6434 (2005).

43. M. Euerby, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–6, 4 March 2010.

44. R. Henry, Pittcon 2010, Orlando, Florida, USA, paper no. 2890–6, 4 March 2010.