Locating Precision Problems

Too much variability in your liquid chromatography method? Here's a look at how to track down the source of the problem.

Sometimes, our liquid chromatography (LC) methods do not perform with the level of precision that we need or expect. When this happens, one or more factors may be contributing to the observed lack of precision. In this month's instalment, we'll see how method precision is determined and some of the factors that influence it. Armed with this information, we should be able to track down the source of problems and, hopefully, correct it.

Before we start, a word about nomenclature. We usually talk about the precision of a method or a measurement, but what we actually measure is the imprecision — lack of precision — or how much error there is in the measurement. So, when we say that a method has 2% precision, we really mean it has 2% imprecision. And what does this mean? Most commonly, imprecision is stated as ±1 standard deviation, with the assumption that the data are normally distributed (unless otherwise stated). From a statistical standpoint, this means that the above example would tell us that the data are within ±2% of the mean approximately 68% of the time, or within ±4% of the mean 95% of the time. Thus, 27% of the time (95%–68%) we would expect the data to be 2% to 4% from the mean. It is important to realize that a stated value for imprecision does not guarantee that the data will fall within any specific limits, but instead gives information about how tightly the data are expected to cluster about the mean value. This is why multiple replicates (typically 6–10) are needed to determine imprecision. Imprecision is most commonly stated in units (millilitres, minutes, milligrams, and so forth) or as percentages. Usually, percentages are stated as the coefficient of variation(CV) or relative standard deviation (RSD), which are equivalent terms: standard deviation divided by the mean. These can be expressed as decimal values or as percentages. I'll use CV in this discussion.

Multiple Sources of Error

Usually, there are several sources of imprecision, or error, in a method. For example, there are potential errors in sampling, sample preparation, injection, chromatography and data analysis. Generally, we assume that these are normally (randomly) distributed, so we can combine them to get the overall imprecision by taking the square root of the sum of squares of each individual source:

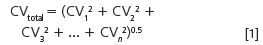
Here, the subscripts refer to the variability of each individual contribution. To have a minor role (< 15%) in the overall imprecision, CV any individual contribution should be no more than 0.5 × CV_total. This gives us a practical guideline of what to watch for when we are trying to isolate a source of error or reduce the overall variability of a method.

To illustrate this, I'll use an example that we use in our LC classes. Let's assume that we need the overall method imprecision to be no more than ±2%, which is to say, CV_total, ≤ 2%. To establish the method precision, we weigh, extract, and analyze 6–10 nominally equivalent samples and find that the standard deviation of the peak areas is ±3.2%. For this example, we'll consider all the sources of error to be included in weighing, sample preparation, injection and integration. We can get a good estimate of each of these contributions, either directly or indirectly, with some simple experiments and estimates. An estimate of weighing error could be obtained by weighing an amount of a strongly UV-absorbing compound equivalent to the sample weight, such as 15 mg. Make six replicate weighings and dilute each in an appropriate solvent and volume, for example, 100 mL of water in a 100-mL volumetric flask. Then check the absorbance with a UV spectrophotometer for several replicates of each sample. By using a different analytical technique, a large dilution volume, and multiple samples and replicates, we have eliminated the chromatographic influences and, we hope, minimized other errors. No matter what you do, you won't eliminate all errors, but this is a good try. Injection error can be checked by making multiple injections of the same sample vial and calculating the standard deviation of the peak area. Integration error can be estimated by dividing the signal-to-noise ratio (S/N) into 50 (1):

where the signal is the peak height measured from the middle of the baseline noise to the top of the peak and the noise is the peak-to-peak baseline width. Sample pretreatment error is difficult to measure directly, but if we know the other contributions, we can rearrange a form of Equation 1 and calculate it:

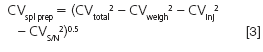
where the various subscripts represent sample preparation (spl prep), weighing (weigh), injection (inj), and signal-to-noise (S/N). If we measured CV_weigh = CV_inj = 0.5% and CV_S/N = 1%, we get CV_{spl prep} = 3.0%.

Reducing Error

There are (at least) two ways to go about reducing method error. I'm always one for trying the easy things first, so let's do that here. Consider uncertainty due to weighing, sample pretreatment, injection, and signal-to-noise ratio. Which are easy to reduce? The answer is everything except sample pretreatment, which can be a lot of work to improve. So, let's reduce the other factors and see what happens. Weighing error is easy to reduce.

Generally, the error in an analytical balance is fairly constant at different weights, so if we can weigh out more sample, the percent error should drop. Similarly, much of autosampler error is constant, whether we inject 1 μL or 100 μL, so again, a larger injection should reduce the percent error. If we weigh out more sample and inject more, it is likely that the peaks in the chromatogram are going to be larger, increasing the signal while having no affect on the noise, so this will reduce the S/N error. If we reduce each of these sources of imprecision to 0.1%, how does this affect the overall method imprecision?

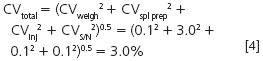
Oops, it looks like the easy way out didn't give us much return on our investment! We reduced the imprecision only from 3.2% to 3.0%, hardly enough for our 2% target value.

What about the hard way? Let's address sample pretreatment. Perhaps we can improve the imprecision by using an internal standard to compensate for losses, modify an extraction or evaporation step, or make some other change in the sample preparation process. If we can reduce the sample pretreatment error from 3.0% to 1.0% and not change any of the other sources of error, how does this change the overall method performance?

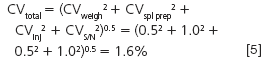
You can see that by reducing the sample preparation error, we cut the overall method imprecision in half.

Now we can add a couple more practical rules of thumb to our collection. First, the overall imprecision will never be smaller than the largest individual imprecision. For example, with sample-preparation imprecision of 3.0%, the overall method will never be more precise than 3%, and most likely will be larger. Second, focus on the largest source of imprecision first when trying to improve method performance. It did no good to address the easy factors first. We only found effective results when the largest source of imprecision, sample preparation, was attacked. After you have reduced a factor below the critical level of 0.5 × CV_total, you can look for the next largest source of error.

A Practical Example

I recently received an e-mail from a reader who had a problem with method precision in an isocratic, reversed-phase method for a formulated drug product. The formulation contained an additive to help stabilize it for the delivery process, but caused shortened column lifetime if it was not removed before analysis. Evaporative lightscattering detection (ELSD) was used. This scientist measured the method imprecision based on recovery of the active compound from the formulation. The overall method imprecision was ±5%, which was more than desired, so the reader was looking for ways to reduce the uncertainty.

The need to remove the additive means that sample preparation was involved; the reader didn't specify, but I suspect it was solid-phase extraction (SPE) or liquid–liquid extraction (LLE). ELSD also throws additional uncertainty into the mix when compared to the more common UV detection. The first thing that I would do here is to check the laboratory records for performance and calibration checks, and repeat any that may need to be updated. Specifically, are the analytical balance and pipettes in calibration? Has the LC system undergone a performance qualification check with a UV detector, such as the one described in reference 2? Such a check will test the system under best-case conditions, but it will assure you that the autosampler imprecision is small (for example, < 0.5%) and that there aren't other basic instrument problems. Has a similar performance check been performed on the ELSD detector? What is the normal level of imprecision for the detector? If it is 5%, there isn't much hope for reducing method imprecision, but if it is 2% or less, performance improvements may be possible.

After I was confident that the basic LC system was operating properly and not a major source of imprecision, I would start under ideal conditions and move to the method conditions in a stepwise fashion to see if I could figure out where the problem originated. A good place to start would be to make up a solution of reference standard of the drug at the normal concentration and make multiple injections with the same volume as normally used, from a single vial of standard. This would give a value for the variability of the injector, chromatography system, detector, and data processing. Because of the non-linear nature of ELSD, it might be a good idea to repeat this experiment over the expected concentration range of real samples. Compare absolute area precision as well as results obtained using a calibration curve to see if the calibration curve might be the problem (such as using the wrong calibration model). I would then repeat the same experiments, but use a formulated product as the sample source. If possible, extract a single large sample, or alternately, extract several replicates and combine the extracts to obtain sufficient volume for multiple injections. How does imprecision change when the formulation is used instead of the reference standard? Does this give you an idea of the problem source? If imprecision increases, it must be due to the additional materials present in the extract, not the sample-preparation process, because injecting a homogeneous extract eliminates sample-preparation variations.

Next, I would perform replicate extractions of a single homogeneous sample. Depending on the formulation, excess sample may be available to extract multiple aliquots; otherwise it may be possible to combine and homogenize several individual samples to create a larger, homogeneous sample source for multiple extractions. Analysis of these samples will help to identify if sample preparation problems are present. Multiple injections (for example, n = 3) may help isolate injection-to-injection variability from extraction-to-extraction variability. Is an internal standard being used? Most of the time, when multiple sample-preparation steps are involved (for example, extraction, evaporation, and reconstitution), an internal standard will reduce imprecision. Check the results with and without using the internal standard for correction. I've seen cases where the internal standard made things worse because there were errors in the way the internal standard was added to the sample. If no internal standard is present, you may be able to use a second peak in the sample as a surrogate internal standard. Track the ratio of the area of this peak to the analyte to see if the ratio is more consistent than the area of the analyte alone. If this is the case, an internal standard should be added to the method.

By breaking down the problem so that experiments progress from ideal to real, you should find a particular step that results in a large increase in imprecision. You can use the techniques discussed in the previous section to help estimate the contribution of various steps to the overall method imprecision. This, then, will help you decide which factors need to be addressed to reduce overall method imprecision.

Rules of Thumb

Sooner or later we'll all encounter a method that has unacceptably large imprecision. This discussion has looked a little at the theory of how errors are combined to give the overall method imprecision. We then looked at a hypothetical example as a way to illustrate the contribution of errors of different magnitude. The practical example at the end helped to show how to start from the best-case of instrument-performance checks and then work through from a reference standard to a complex sample-preparation process in an effort to isolate different sources of uncertainty in a method. From this discussion, we can list five guidelines for isolating imprecision problems:

• If we assume errors are random, the overall uncertainty of a method is the square root of the sum of squares of the individual contributions to uncertainty (Equation 1).

• To have an insignificant (≤ 15%) contribution to the overall error, an individual source of error can be no more than 50% of the desired method imprecision.
• The overall method imprecision will never be smaller than the largest individual contribution to that error.
• As a result of rules 2 and 3, we should first seek to reduce the largest individual source of error, especially if it is > 50% of the target method uncertainty.
• To isolate the source of imprecision, start from a simple, ideal, well-behaved system and sample, then add complexity in a stepwise fashion until the problem source is identified.

(1) L.R. Snyder, J.J. Kirkland and J.L.Glajch, Practical HPLC Method Development, 2nd Ed. (Wiley, Hoboken, New Jersey, 1997) p. 71.

(2) G. Hall and J.W. Dolan, LCGC N. Amer. 20(9), 842–848 (2002).

"LC Troubleshooting" editor, John Dolan, is vice president of LC Resources, Walnut Creek, California, USA. He is also a member of LCGC Europe's editorial advisory board. Direct correspondence about this column should go to "LC Troubleshooting", LCGC Europe, 4A Bridgegate Pavillion, Chester Business Park, Wrexham Road, Chester CH4 9QH, UK, or e-mail the editor, Alasdair Matheson, at amatheson@advanstar.com