Is Golay’s Famous Equation for HETP Still Relevant in Capillary GC? Part 2: Assumptions and Consequences

This instalment is the second part of a discussion on the origins and uses for determining the height equivalent of a theoretical plate (HETP) calculations in gas chromatography (GC). This month, we discuss the good and challenging consequences of the Golay theory, its relevance, and some alternatives. Many of the variables that chromatographers view as independent have some interdependence, and we see several limitations of the theory. The complex relationships between HETP and temperature present a particular challenge when thinking about temperature programmed GC compared to isothermal GC. This column concludes with comments regarding the continued relevance of this classical theory.

In the January 2022 instalment, we examined Golay’s famous equation describing the height equivalent to a theoretical plate (H or HETP), one of the most common measures of capillary column performance (1). The equation originally derived by Golay is shown below in equation 1. A commonly used simplified form, which was developed sometime later, is likely a misinterpretation of Golay (2). As in last month’s column, equation 31a from Golay’s paper is used here.

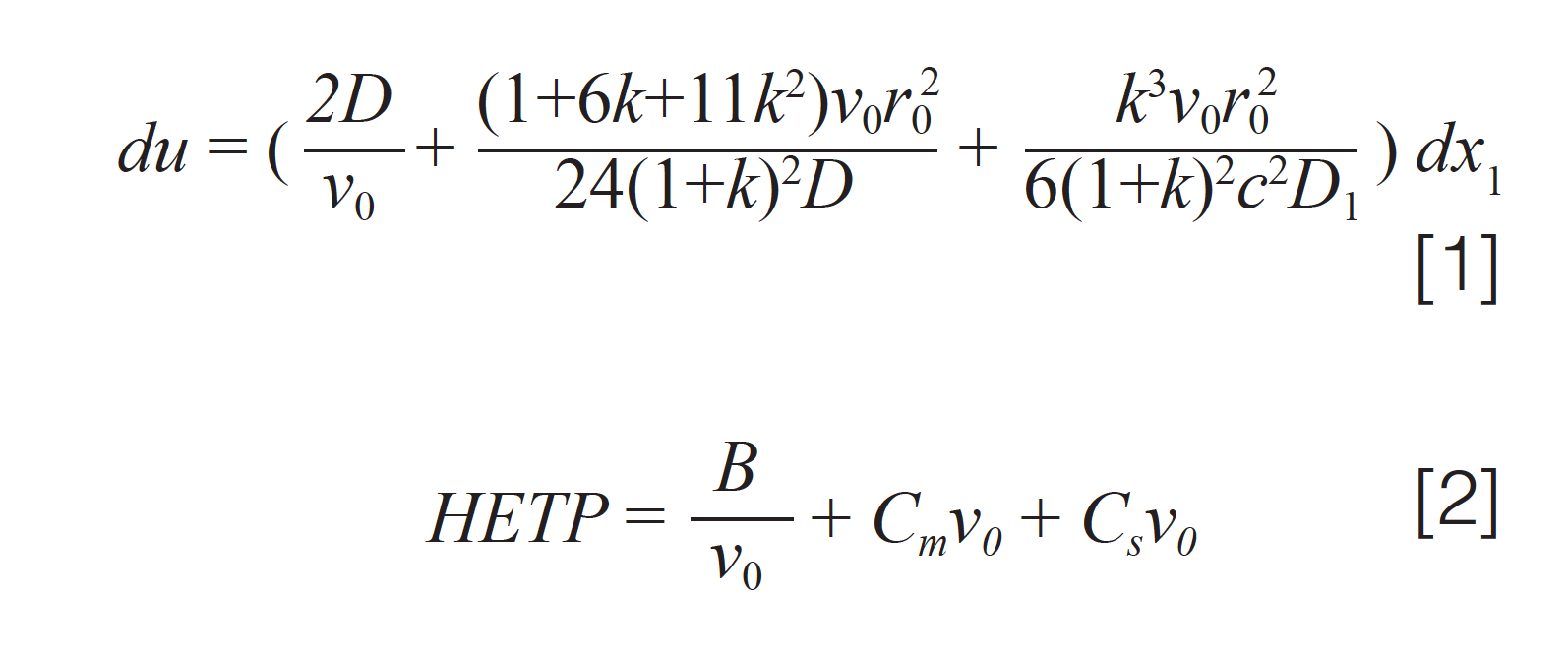
Definitions of the variables are discussed in detail in last month’s instalment. As we concluded last month, the many variables in equation 1 are themselves interdependent in ways that are not always obvious and can cause confusion for chromatographers in understanding and using the equation to assist in column and method optimization. Next, we ask three key questions about equations 1 and 2 that lead to comments about the use and relevance of the two equations.

1. Is the average carrier gas velocity independent of the other variables?
2. What is the effect of the polynomial expressions of the retention factor k on the mass transfer terms?
3. What about temperature and the relevance to temperature programming?

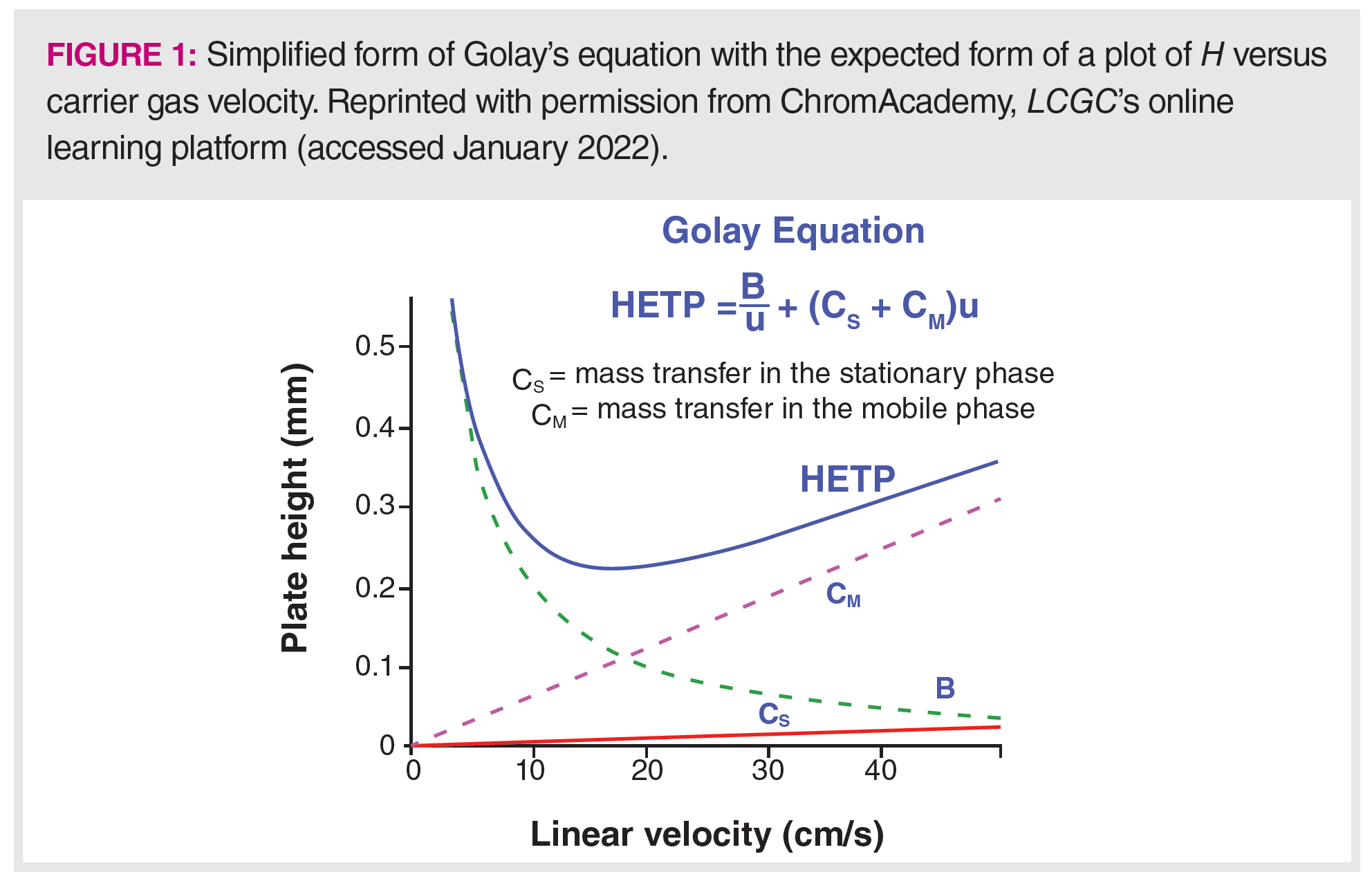
Figure 1 shows a simplified “Golay plot” of the form seen in countless textbooks on analytical chemistry, chromatography, and in nearly every course on gas chromatography (GC) that discusses theories. In experimental work, such plots are often used to evaluate new columns and methods, to compare experimental conditions, or to make a claim that a column is performing adequately. In this column, we use the three above‑mentioned questions to critique this plot to better understand why the literature includes many experiments that do not appear to follow this behaviour, and to answer our larger question of the relevance of Golay’s equation and these plots in today’s capillary GC. Interestingly, the version of equation 2 presented in Figure 1, which seems to be the most common presentation, has the two mass transfer terms reversed in order from Golay’s original equation.

Is the Average Carrier Gas Velocity Really Independent of the Other Variables?

In making plots as seen in Figure 1,H is plotted against the average carrier gas velocity (u or v₀) as seen in equation 2, and the expected shape of the plot as the carrier gas velocity increases is seen in Figure 1. Although this behaviour is seen in many cases, it is not universal. The first example of this is seen in the same initial symposium where Golay presented and discussed equation 1, following a paper by Dujkstra and de Goey. Sjenitzer commented on this paper and showed a plot of N, the number of theoretical plates versus inlet pressure, determined at several stationary phase film thicknesses (3). Although some of the plots showed the behaviour illustrated in Figure 1, many of them did not, with a variety of curve shapes.

An example challenge with using the simplified form shown in equation 2 is that the average carrier gas velocity influences the other variables, most notably the retention factor, k, which appears in both mass transfer terms. We are reminded of the definitions of k and its relationship to the gas hold-up time, t_M, and the average linear gas velocity, v₀, in equation 3:

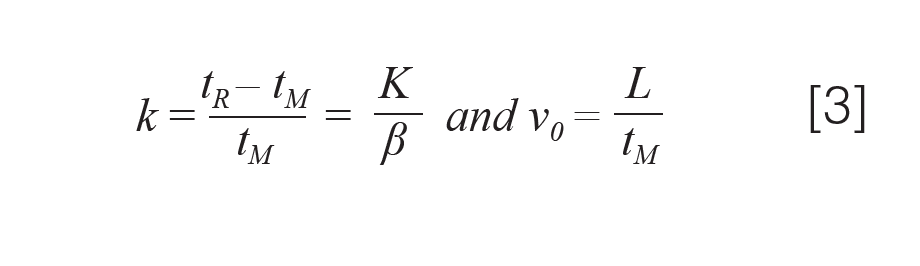
Both the average carrier gas velocity and k are calculated in practice from t_M, which itself is a complex function of carrier gas properties, column dimensions, and the inlet and outlet pressures (4,5). We see that k and
t_M are closely related; therefore, k and v₀ are also closely related.
As a result, the use of v₀ in equation 2, as a variable independent of the other terms in the more detailed equation 1, is clearly an oversimplification that may cause confusion.

Since the average carrier gas velocity itself is a derived quantity, a complex function of column dimensions, identity of the carrier gas, and the inlet and outlet pressures, and those same factors also influence the retention factor and the gas phase diffusion coefficient (D), we see that the relationship between H and v0 is much more complex than implied by equation 2.

What is the Effect of the Polynomial Expressions of the Retention Factor k on the Mass Transfer Terms?

The interesting polynomial functions of k, seen on the two mass transfer terms, are often overlooked as impacting the determination of H and the resulting determination of N, the number of theoretical plates. We know that k is analyte-, temperature-, and stationary‑phase dependent, yet plates and plates per metre are often reported with little specifics. As an example, Figure 2 shows the dependence of the polynomial function of k, with k ranging from 1 to 20, as seen in the mobile phase mass transfer term in equation 1.

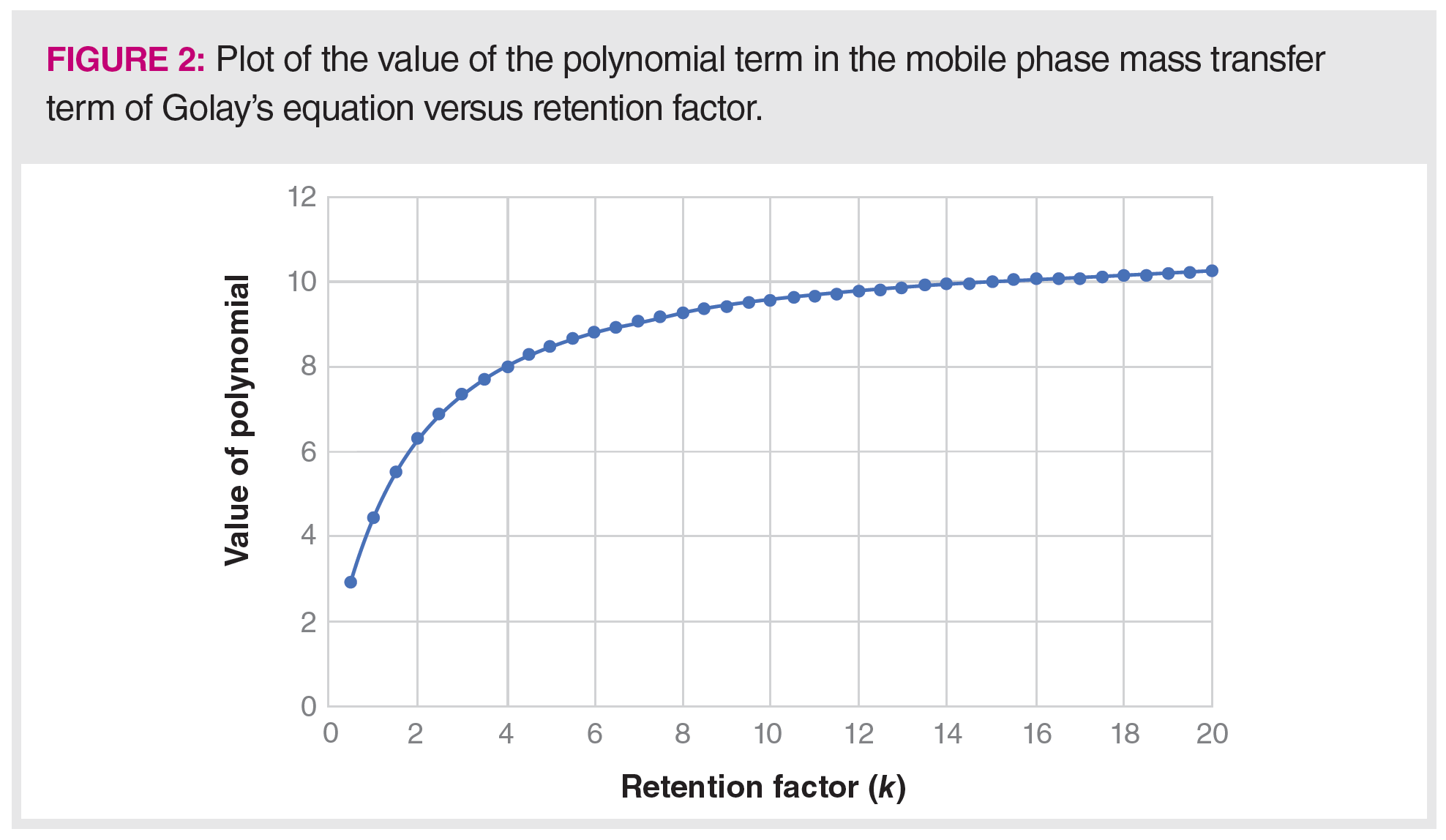
Note in Figure 2 that the result varies considerably with retention factor with a low of approximately 3 for k = 0.5 to approximately 10 for k = 10–20.
A larger k, which means longer retention times, results in the function roughly approaching a constant, indicating little influence of the retention factor on H and by extension N. As k gets smaller, the polynomial term also gets smaller with greater influence seen at smaller k.

There are several practical consequences of this result.
First, because k is analyte dependent, each analyte sees a different result
for the polynomial and, therefore, a different H and N. Often, N is quoted for a particular column, but this must be stated with the caveat that it was determined for a specific analyte under a specific set of instrumental conditions. In Figure 1, we see that mobile phase mass transfer is often the dominant term in determining H and N. In Figure 2, we see that k, on which the mobile phase mass transfer term depends, may vary by as much as a factor of three, depending on experimental conditions. Therefore, the actual number of theoretical plates experienced by an analyte in practice may vary significantly from the number reported for the column, and N can be expected to vary significantly from analyte to analyte and condition to condition.

A similar impact is seen in the k-related terms in the stationary phase mass transfer term. This term also has a polynomial function of k and, largely because of the presence of the partition coefficient in the denominator, generally has a smaller impact on H and N, which is seen in Figure 1. When the retention factor term and the partition coefficient are combined using equation 3, the result is a polynomial term that ranges from 0.2 at k = 0.5 to approximately 0.04 at k = 20.

What About Temperature and the Relevance to Temperature Programming?

When van Deemter and Golay developed the theory of band broadening in the 1950s, nearly all practical GC was done using packed columns and isothermal analysis. Both equations 1 and 2 assume constant temperature, so this is another variable that must be controlled if experiments are to be comparable. Prior to the development of fused-silica capillary columns in the late 1970s, capillary GC was seen as more of a novelty than a technique for routine analysis. Today, almost all laboratory gas chromatographs are capable of temperature programming and most capillary column-based methods are temperature programmed. As discussed in an earlier “GC Connections” instalment, the peaks in a temperature-programmed separation do not broaden as rapidly as they do in an isothermal separation. In that article, I raised the question, “Why are all those peaks so sharp?” (6). Equation 1, as it assumes constant temperature, does not fully explain this, but the concepts seen in the three terms and the variables can provide a qualitative discussion.

Equation 1 provides some qualitative insight about why the peaks in temperature programming appear sharper than in an isothermal analysis with similar retention times. The sharp peaks indicate that the rate of band broadening in temperature programming must be much smaller (slower) than in isothermal analysis. As seen in Figure 1, the mobile phase diffusion term is relatively low and nearly constant at most practical carrier gas velocities and temperatures, so the main impact on H would be seen in the two mass transfer terms. We also have seen that the mobile phase mass transfer term has the greater impact on H. Higher temperatures reduce k, which diminishes the value of the polynomial and increases D, reducing the overall value of the mobile phase term. Therefore, the mobile phase mass transfer term lowers H and leads to a reduction in the rate of band broadening and sharper peaks.

Is Golay’s Equation Still Relevant?

Golay’s equation, shown in equation 1, that was developed in the 1950s is still relevant today, although the context in which we use and think about it has changed. With most methods employing temperature programming, the practical utility of Golay plots and plate height calculations today is limited. The need for the exact matching of conditions, such as temperature, carrier gas, flow rate, and analyte, make column‑to‑column comparisons difficult, and the requirement for constant temperature makes conclusions about column performance based on these plots not readily translatable to temperature-programmed methods. The simplification of H plotted as a function of v0, as seen in equation 2, is an oversimplification that does not do proper justice to the many interrelationships between the many variables in the original equation and should be used with caution. Equation 2 would be better expressed as:

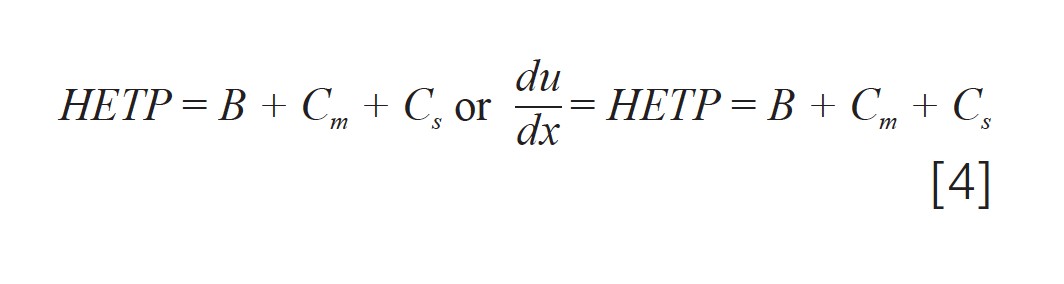
with the carrier gas velocity included in each term, not expressed as an independent variable, which now expresses HETP as a rate and then requires discussion of each term tailored to the experiment being performed.

Golay’s original intent is why his equation is still relevant today.
It describes the separation process in measurable terms based on physical properties of the column, carrier gas, and analyte. Unless experimental conditions are carefully controlled to ensure an “apples to apples” comparison, we should be cautious when using Golay’s equation to attempt direct comparisons of column performance from one column or one set of instrumental conditions to another. We should avoid extending conclusions about column performance derived from Golay’s equation under isothermal conditions to temperature-programmed conditions. Finally, as an extension, determinations of the number of theoretical plates in a column, or the number of plates per metre, are only valid for the exact analyte and isothermal experimental conditions under which the determination was made. We should be careful using such data to compare the performance of one column to another, especially if we intend to conduct temperature-programmed analysis. In spite of these limitations, Golay’s equation remains relevant in helping us understand the many complex processes that relate to the rate of band broadening in chromatography.

References

1. N.H. Snow, LCGC Europe 35(1), 21–25 (2022).
2. M.J.E. Golay, in Gas Chromatography, D.H. Desty, Ed., (Butterworths, London, UK, 1958), pp. 36–55.
3. C.S.G. Phillips and F. Sjenitzer, in Gas Chromatography, D.H. Desty, Ed., (Butterworths, London, UK, 1958), pp. 62–64.
4. S.P. McCann, H. Rana, B.A. Handzo, and
   N.H. Snow, LCGC Europe 33(3), 127–134
   (2020).
5. L.M. Blumberg, in Gas Chromatography, 2nd Edition, C.F. Poole, Ed., (Elsevier, Amsterdam, The Netherlands, 2021), pp. 48–95.
6. N.H. Snow, LCGC Europe 32(7), 370–376 (2019).

About The Author

Nicholas H. Snow is Founding Endowed Professor in the Department of Chemistry and Biochemistry at Seton Hall University, and Adjunct Professor of Medical Science. During his 30 years as a chromatographer, he has published more than 70 refereed articles and book chapters and has given more than 200 presentations and short courses. He is interested in the fundamentals and applications of separation science, especially gas chromatography, sampling, and sample preparation for chemical analysis.His research group is very active, with ongoing projects using GC, GCÐMS, two-dimensional GC, and extraction methods including headspace, liquidÐliquid extraction, and solid-phase microextraction. Direct correspondence to: amatheson@mjhlifesciences.com