The Perfect Method, Part 7: The Gradient Shortcut

For the last six months, "LC Troubleshooting" has been concentrating on the process for the development of isocratic methods (those for which the mobile phase composition is constant throughout the run). This worked through the sequence of goal setting,¹ selecting the right starting conditions,² adjusting retention,³ changing peak spacing^4,5 and fine-tuning the column efficiency.⁶ Hopefully you have gained additional insight into the liquid chromatography (LC) process, as well, so your methods will be less likely to fail and will be easier to troubleshoot.

The first step in getting an acceptable separation is to get the retention times in the right general region.³ This is often is accomplished by changing the mobile phase organic content (%B) for a reversed-phase separation in 10% increments from 100% organic until the retention factors k are in the range of 1–20, or better yet, 2–10. Because peaks move in a regular fashion as the mobile phase strength is changed, we can generalize the effect of solvent strength as "The Rule of Three". This states that the k-values change by approximately three-fold for each 10% change in organic. Because k changes three times per 10% change, a 20% change will result in approximately 3 × three-fold, or roughly 10-fold. Using such guidelines and a little common sense, we can usually find isocratic conditions that give us the 1 < k < 20 or 2 < k < 10 retention times in three to five runs. Wouldn't it be nice to be able to find these conditions in the very first run? Well, with the help of a gradient scouting run, you usually can. The use of a gradient scouting run to speed isocratic method development is the subject of this month's "LC Troubleshooting."

Where to Start?

A very efficient way to start an isocratic method development project is to make the first run as a scouting gradient run. With isocratic runs, you cannot often anticipate where peaks will come out in the first chromatogram, so you are forced to start with a solvent that is too strong (for example, 90% or 100% B). Then you work to weaker solvents in 10 or 20% steps using "The Rule of Three" for a guide until you achieve 2 < k < 10 for your sample. With gradient elution, you can predict in advance conditions that are likely to give the gradient equivalent of 2 < k < 10. This will occur for small molecules (molecular weights < 1000 Da) for full-range gradients that comprise ≈25 column volumes of solvent. For example, if we use the column recommended for starting with an LC–UV method,² a 150 mm × 4.6 mm column packed with 5 μm particles, the column volume is approximately 0.01 × the column length (in millimetres), or ≈1.5 mL. This means that the gradient should be ≈37.5 column volumes; a 20 min gradient at 2 mL/min (40 mL volume) is close enough. For an unknown sample, we don't know the polarity range, so it is best to run a full-range gradient of 5–95% or 5–100% organic solvent (keep the percentage of organic solvent greater than 5% to avoid column dewetting). An example of such a gradient scouting run is shown in Figure 1 (the chromatogram is only shown until the last peak has been eluted).

Figure 1

Evaluating the Scouting Run

The first question after we run the scouting run should be, "Is a gradient or an isocratic run best for this sample?" An easy way to make this evaluation is to examine the fraction of the run time occupied by peaks. If the peaks take ≤25% of the run time, an isocratic run is the best choice. If ≥40% of the run is occupied by peaks, a gradient is advised. Between these limits, either an isocratic or gradient run can be possible.

In the instance of Figure 1, the first peak is eluted at ≈10 min and the last peak at ≈12 min. So (12 – 10)/20 = 10%, which is less than 25%, so an isocratic run is recommended. There are several ways to select the isocratic conditions at this point, but one of the easiest is to use an Excel spreadsheet calculator that you can download for free from the LC Resources website (reference 7, go to the "Resources" page and download the file "scouting_gradients.xls").

The use of this calculator is shown in Figure 2. In the top section, fill in the run conditions for the scouting run. In this case, a 150 mm × 4.6 mm (15 cm × 0.46 cm) column was used. The equipment dwell volume was 1.5 mL and the flow-rate was 2.0 mL/min. The gradient was run from 5 to 100% organic in 20 min. At the bottom left, enter the retention times for the first (10.0 min) and last (12.0 min) peaks. The calculator then recommends the type of method for the next run (isocratic for this example) and conditions for the run (44% organic). I usually round this number to the nearest 5% for convenience. If you insist on running a gradient method, the conditions for the next run are shown (40–55% in 3 min), which adjusts the gradient to remove most of the wasted time before the first peak and after the last peak are eluted.

Figure 2

The calculator requires that you know the dwell volume of your LC system. This is the volume from the point the solvents are mixed until they reach the head of the column. The calculation should be done for every LC system, and is straightforward using the directions in references 8 or 9, Section 4.3.1.2. High-pressure-mixing systems typically have dwell volumes in the 1.5–3.0 mL range, whereas low-pressure-mixing systems are a little larger, with typical volumes of 2.5–4.0 mL. LC systems designed for small-volume applications such as LC–mass spectrometry (MS) often have dwell volumes of 0.2–0.5 mL.

The First Isocratic Run

After the scouting gradient has been run and isocratic conditions have been determined to be appropriate, it is time to make the first isocratic run. The chromatogram for the isocratic conditions recommended from Figure 2 (rounded to 45% organic) is shown in Figure 3. The column dead time t₀ is (1.5 mL/2.0 mL/min) ≈ 0.75 min, so k = ([t_R – t₀]t₀) can be calculated from the retention times t_R of the first (1.8 min) and last (7.6 min); 1.4 < k < 8.9. This is within the 1 < k < 20 and close to our target of 2 < k < 10.

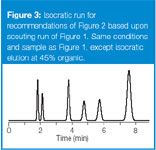
Figure 3

The run of Figure 3 can be satisfactory for many applications (resolution ≈2.0), but further fine-tuning might be desirable, as described in earlier instalments of this series. It is unlikely that the first isocratic run will be as good as in this example, but the retention should be in the right range to start fine-tuning the separation. It is highly unlikely that you would be as close to a 1 < k < 20 separation in two runs using the 100%, 90%, 80%... technique, so the gradient scouting run is a faster way to home in on the best isocratic conditions.

What About Gradients?

The gradient scouting run, as used in the previous example, led us to an acceptable isocratic run in just two injections. Another strong advantage of the gradient scouting run is that it yields useful data if isocratic conditions are not possible. If the retention range for the sample is broad, such that the ratio of k-values for the first and last peak exceeds 20, a gradient method usually is required. If you start method development with isocratic steps, you will realize after a few runs that the sample is too complex for isocratic separation, but the data you gathered isocratically will be of no use. You will have to start over with gradient runs. By using the gradient scouting run, you can evaluate the "isocratic or gradient" question based upon the initial run and proceed with the appropriate method development strategy with no wasted runs.

We've spent enough time over the last few months discussing isocratic method development and I would like to get back to some more traditional troubleshooting problems, so we'll leave gradient method development for a future discussion. A good resource for gradient method development is reference 9, especially chapter 3.

Conclusions

In this series of columns on method development for isocratic, reversed-phase separations, we've seen that a systematic approach will yield results in an efficient manner. The use of a gradient scouting run, as outlined here, can be a real time-saver at the beginning of the method development process. It can give us an idea of the complexity of the sample and using tools such as those shown in Figure 2, we can determine if an isocratic or gradient method will be required, as well as recommended conditions for the next isocratic (or gradient) run.

"LC Troubleshooting" editor John W. Dolan is vice-president of LC Resources, Walnut Creek, California, USA and a member of LCGC Europe's editorial advisory board. Direct correspondence about this column to "LC Troubleshooting", LCGC Europe, Advanstar House, Park West, Sealand Road, Chester CH1 4RN, UK.

Readers can also direct questions to the Chromatography Forum at www.chromforum.com

References

1. J.W. Dolan, LCGC Eur., 20(9), 438–443 (2007).

2. J.W. Dolan, LCGC Eur., 20(10), 504–509 (2007).

3. J.W. Dolan, LCGC Eur., 20(11), 568–573 (2007).

4. J.W. Dolan, LCGC Eur., 20(12), 622–625 (2007).

5. J.W. Dolan, LCGC Eur., 21(1), 20–23 (2007).

6. J.W. Dolan, LCGC Eur., 21(2), 78–83 (2007).

7. www.lcresources.com

8. J.W. Dolan, LCGC Eur., 19(6), 336–343 (2006).

9. L.R. Snyder and J.W. Dolan, High-Performance Gradient Elution (Wiley, New York, New York, USA 2007).