Column Diameter, Linear Velocity and Column Efficiency

I recently had a question regarding some changes that took place in the 2009 edition of the US Pharmacopeia. In USP 32, General Chapter 621,¹ the adjustments allowed to meet system suitability for liquid chromatography (LC) methods include a change in column internal diameter of ±25%. A change was made in USP 32 Supplement 2.² This stated that column internal diameter "can be adjusted provided that the linear velocity is kept constant." The person was not sure how this adjustment of linear velocity should be made and wondered about what effect it would have on column efficiency.

Adjustment of Flow Rate

Much of the band broadening that takes place within an LC column is a result of slow diffusion of the analyte in and out of the pores in the column packing. This means that the mobile phase flow rate can have an affect on the volumetric width of a peak. By volumetric width, I mean the peak width in units of volume (for example, millilitres or microlitres), not time. In the days when 10 μm diameter particles were used as column packing, a noticeable reduction in column efficiency could be observed when the flow rate was increased.

The smaller the particle diameter, the less the dependence of column efficiency upon flow rate. Although it is easy to demonstrate a loss in efficiency with an increase in flow rate for very well-behaved analytes with 3 and 5 μm diameter particles, a two-fold change in flow rate is rarely noticed with real applications. With sub-3 μm particles, flow rate has little influence on column efficiency, even with well-behaved compounds.

In this discussion, I have referred to flow rate, but the important variable is not flow rate, but linear velocity. Linear velocity is the speed at which the mobile phase travels through the column, for example, in millimetres per second. For comparison of equivalent conditions between columns of different internal diameters, the linear velocity should be kept constant. To keep linear velocity constant, the flow rate should be adjusted in proportion to the column cross-sectional area, which is directly proportional to the square of the ratio of column diameters. For the current discussion, let's consider two cases. The first is a change from a 4.6 mm i.d. column to a 2.1 mm i.d. column:

(4.6/2.1)2 = 4.8 ≈ 5

and the change from 4.6 mm to 1.0 mm:

(4.6/1.0)2 = 21.2 ≈ 20

In both cases, we'll consider the approximations as close enough for practical work and certainly easier to remember and use for mental calculations.

This means that for equivalent linear velocities, a change from a 4.6 mm i.d. column operated at 1 mL/min to a 2.1 mm i.d. column would require a flow rate adjustment of five-fold, or to 1.0/5 = 0.2 mL/min. A change to a 1.0 mm i.d. column would mean a new flow rate of 1.0/20 = 50 μL/min.

The Old Allowance

USP 32 allowed a change in column diameter of ±25%.¹ This meant that a 4.6 mm i.d. column could be exchanged for any column in the 3.45–5.75 mm i.d. range. I suspect that this specification was originally written to allow the old Waters μBondapak 300 mm × 3.9 mm column to be used instead of the 4.6 mm i.d. versions. USP 32 also allowed a ±50% change in flow rate. The 3.9 mm i.d. column would require a flow-rate reduction of 30% for constant linear velocity, so the necessary flow-rate change was covered. Note, though, that the flow-rate change was not required by USP, so a significant change in linear velocity was allowed. Today, however, the most popular column internal diameters are 4.6, 2.1 and 1.0 mm, so the ±25% diameter-change allowance eliminated the option of using smaller-internal-diameter columns. It is clear that a change in the USP was needed.

The New Allowance

The change in USP 32, Supplement 2 at first seems more complicated by introducing the linear velocity,² but actually, it gives more flexibility and ensures a more equivalent result than the old allowance. Now any column diameter can be used, so the 2.1 and 1.0 mm i.d. columns can be used in addition to the 3.9 mm i.d. ones. In addition, the adjustment in linear velocity means that the columns will be operated under more similar chromatographic conditions than before. By properly adjusting the linear velocity, the column pressure and analyte retention times should be the same when column diameter is changed.

Column Efficiency

What wasn't addressed in the original question was why one would want to use a column of different diameter. There are two primary advantages, decreased mobile-phase consumption and a reduction in peak volume. If the flow rate is adjusted for constant linear velocity, as discussed earlier, the retention times should be the same when column diameter is changed, so the sample run time will be unchanged. If the run time is the same and the flow rate is reduced, less mobile phase will be used. This is attractive, especially in these days of high acetonitrile prices.

The peak volume (peak width in volumetric terms) drops with the reduction of the cross-sectional area of the column, or square of the change in diameter. This translates into proportionally taller peaks, assuming that the same mass of sample can be loaded onto the column, which may or may not be true. Thus, moving from a 4.6 mm i.d. column to a 2.1 mm column should reduce peak width by five-fold and increase peak height by the same amount (assuming the same mass of sample is injected).

This leads to the second part of the original question, regarding how a change in column diameter affects column efficiency. In theory, there should be no dependency of efficiency upon column diameter, but from a practical standpoint, narrower columns are usually less efficient than larger-diameter ones.

The primary factor in determining the column efficiency is the number of particle diameters in the length of the column. Under ideal conditions, a well-packed column should have a plate height H equivalent to approximately two particle diameters d_p. The column efficiency, or column plate number N is calculated as

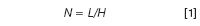
where L is the column length. For a 5 μm particle (d_p), two particle diameters would give H = 10 μm = 0.01 mm. Packed in a 150 mm-long column, this would give

N = 150/0.01 = 15000

You might be able to get 15000 plates for a 150 mm × 4.6 mm column mounted on an high performance liquid chromatography (HPLC) system optimized for column testing and using a well-behaved test compound such as toluene or methyl benzoate. However, for real samples on a typical laboratory's HPLC system, most of us would feel very good to get 10000 plates for this column. Even if we used toluene or methyl benzoate, we might get only 12000 plates on the system in the laboratory.

Extracolumn Effects

What is the reason for the reduced plate number on a real HPLC system? Part of it has to do with extracolumn peak broadening. Here's how it works. The width of a peak in a chromatogram can be expressed as

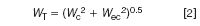
where W_T is the observed peak width at baseline, drawn between tangents to the sides of the peak, W_c is the peak broadening that takes place as the analyte travels through the column and W_ec is the peak broadening outside the column, often referred to as extracolumn effects.

We have all observed peak broadening within the column W_c. For example, with an isocratic separation, the early-eluted peaks are narrower than later-eluted ones. This is because the longer the compound stays on the column, the broader it is. Some other factors related to on-column peak broadening include the particle diameter, column temperature, mobile phase viscosity and analyte diffusion coefficient.

Extracolumn effects include all sources of peak broadening excluding the column itself. These include such things as the injection volume and solvent, the length and diameter of connecting tubing between the autosampler and column and between the column and detector, the detector cell volume and time constant and the data rate of the data system. For the present discussion, we'll consider these as a composite influence. For a conventional LC system, such as the ones most of us use, set up for routine analysis with 150 mm × 4.6 mm i.d. columns packed with 5 μm diameter particles, Wec ≈15 μL is a typical value.

Impact of W_ec on N and R_s

It is an interesting exercise to assess the degradation of the column plate number N and resolution, R_s, for columns of different diameter. In Table 1 I have summarized data for a peak with the retention factor, k = 1. The assumptions in both tables are a column length L = 150 mm; column internal diameter, d_c = 4.6 mm (or as noted); column void volume of 60% of the column volume; flow rate F = 2.0 mL/min for the 4.6 mm column; 5 μm particles for a column plate number, N = 15000 in absence of extracolumn effects; and an extracolumn volume of 15 μL. Data are shown for 4.6, 2.1 and 1.0 mm i.d. columns. I have rounded the displayed values for clarity, so if you are trying to repeat my calculations in a spreadsheet, keep the maximum number of significant figures for all calculations.

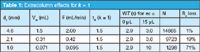
Table 1: Extracolumn effects for k = 1

In the second and third columns of Table 1, you can see the column volume V_M calculated for each column diameter and the flow rate adjustments required to maintain a constant linear velocity. For an early-eluted peak with k = 1 and a 4.6 mm i.d. column, there is a very small increase in peak width resulting from the extracolumn volume. However, the 15 μL of extracolumn volume increases the peak width by more than three-fold for the 1.0 mm i.d. column (2.9 versus 10 s). This reduces the plate number by more than an order of magnitude, and because resolution is proportional to the square root of the plate number, resolution drops by 71%! Most of us consider a drop in resolution of 5% or less to be of little consequence, but it is obvious from the data in Table 1 that use of a 2.1 or 1.0 mm i.d. column with an early-eluted peak will not produce satisfactory results with this LC system.

Table 2 summarizes the impact of 15 μL of extracolumn volume on peaks with larger k-values. It can be seen that more retained peaks are influenced less by extracolumn volume for all column diameters. This is expected, because peak width within the column W_c increases with retention, so with constant W_ec, the observed peak width W_T will be less affected. However, for the chosen chromatographic conditions, the 2.1 mm i.d. column is acceptable (R_s-loss < ≈5%) only for well-retained peaks. The 1.0 mm i.d. column does not produce satisfactory results at any retention time.

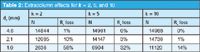
Table 2: Extracolumn effects for k = 2, 5, and 10

A disclaimer should be included here, as on the advertisements for new cars: your mileage may vary. Tables 1 and 2 were calculated based upon the assumption that the 5 μm particle diameter column generated N = 15000. As mentioned earlier, this represents the performance of a well-packed column operating under ideal conditions. It is likely that such a column will generate plate numbers in the 10000 range for real compounds under real analytical conditions. This means that the peaks will be broader, even under the best circumstances, so the impact of extracolumn volume will be less than that shown in the tables. However, the general conclusion is the same: you will have to minimize extracolumn effects if you want to get acceptable results with 2.1 mm i.d. columns on a conventional LC system. Furthermore, it is unlikely that you will get satisfactory performance from 1.0 mm i.d. columns unless you take great care. This will mean limiting injection volume, replacing the detector with one with a smaller-volume flow cell and making other changes to reduce extracolumn effects.

Conclusions

It is fairly simple to make the necessary changes in flow rate to maintain constant linear velocity when changes in column diameter are made. A reduction in column diameter can be useful to conserve solvent and to improve detection limits. However, a drop in system performance, as measured by resolution, might be observed for smaller-diameter columns unless special care is taken to reduce extracolumn effects. From a troubleshooting standpoint, it is tempting to blame poor system performance on the column itself, when the real culprit may be the extracolumn volume of the LC system. A relative insensitivity to extracolumn effects is one reason why the 150 mm × 4.6 mm column packed with 5 μm diameter particles is likely to remain the workhorse column for routine LC work for many years to come.

"LC Troubleshooting" editor John W. Dolan is vice president of LC Resources, Walnut Creek, California, USA; and a member of the Editorial Advisory Board of LCGC Europe. Direct correspondence about this column to "LC Troubleshooting", LCGC Europe, Park West, Sealand Road, Chester CH1 4RN, UK.

For an ongoing dicussion of LC Troubleshooting with John Dolan and other chromatographers, visit the Chromatography Forum discussion group at www.chromforum.org

References

1. United States Pharmacopoeia 32, General Chapter 621, 237 (2009).

2. United States Pharmacopoeia 32 (Supplement 2), General Chapter 621, 4149 (2009).