Are Short Columns Always The Best Option?

Introduction

Many column and instrument manufacturers are promoting small particle columns and high-pressure instruments, but it should never be overlooked that improvements in separation speed and efficiency can also be obtained by an optimal selection of the column length and not only by investing in new high-pressure equipment.

It has been common knowledge since the early days of chromatography^1–4 that the time cost per theoretical plate continuously decreases with increasing mobile phase velocity (i.e., with increasing applied pressure). This can be conveniently illustrated using two basic chromatographic relationships:

which, after dividing the one by the other, readily show that the time needed to achieve one theoretical plate unit, the so-called plate time (t/N), is equal to the ratio of H/u:

Figure 1 shows how Equation 3 transforms the y-axis of a typical van Deemter curve, and how this leads to a plot of plate time (t ₀ /N) versus u0. The obtained end result shown in Figure 1(b) clearly shows that the time needed to generate one theoretical plate is shortest at the highest flow-rate (i.e., at the maximal pressure) and not at the optimal flow-rate. In the present example, the plate generation speed at the maximal velocity is about double the plate generation speed obtained near the optimal velocity. This trend is in fact typical for any van Deemter curve having a high-velocity range wherein the plate heights do not increase more than linearly with the velocity.

Figure 1

This is nearly always the case, except in some special instances where the plate height curves display a convex upward trend in the high-velocity range, for example, because the sampling time of the detector has been too low or because of the occurrence of some high-pressure viscous heating effects.⁵ Hence, the following rule holds in the majority of the cases: if one is to get a given plate number in the shortest possible time, one has to use a column that delivers this given plate number with a flow-rate situated as deep as possible in the C-term regime (i.e., at the highest possible pressure).

Figure 2

This "maximal pressure"-condition is implicitly contained in the expressions underlying the so-called kinetic plot method.^6–8 Briefly, this is a method that incorporates both the pressure drop and the band broadening characteristics of a given particle or monolithic support type into a plot of time versus efficiency N (or peak capacity or resolution). Combining Equations 1 and 2 with the general pressure drop expression:

yields the two following simple kinetic plot expressions:

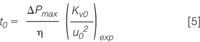
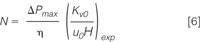
Applying these equations, for example, to the van Deemter data shown in Figure 1(a) yields the kinetic plot curve shown in Figure 2 (red curve). Each data point in this curve originates from one of the experimental data points in the plate height curve and relates to a column with a different length (all data points relate to the same pressure but to a different velocity, hence the related length must vary). The curve in fact links the efficiencies and the t₀-times that can be obtained if one would have a whole battery of columns at its disposal, all filled with the same particle type but with a different length and all operated at the same (maximal) column pressure (i.e., at the lowest time cost for each generated theoretical plate).

Figure 3

One can, however, also establish time versus efficiency plots for cases wherein the column length is fixed while the pressure is varied (in fact this is what one actually does if one establishes a van Deemter curve by testing a column at different flow-rates). In this case, one can simply use Equations 1–2 instead of Equations 5–6.

Applying Equations 1–2 to the plate height data shown in Figure 1(a) and taking L equal to the length of the column wherein the actual van Deemter experiment has been performed, one simply gets the analysis times and the corresponding efficiencies that were obtained in the actual experiment (green curve in Figure 2). Subsequently changing L into another value then gives a prediction of the efficiencies and the related analysis time that can be obtained if one would be using the same type of particles but in a column with a different length (black curves in Figure 2).

Figure 4

If we look closer at these fixed L-curves, [see Figure 2(b)] it can be readily seen how the velocity and the pressure vary along the curves and transit from the B-term (dotted part of curves) into the C-term region by passing over the data point relating to the optimal velocity (cf. the added crosses). It should be noted here that the data points corresponding to the B-term regime are not explicitly shown because the B-term regime should anyhow be discarded in the search for fast separations. Each fixed L-curve reaches the kinetic plot curve at the maximal pressure.

Figure 5

Figure 2 clearly shows that the kinetic plot curve (red curve) of a given support type (with a fixed size and shape) can be considered as the curve enveloping all possible combinations of efficiency and analysis time that can be achieved with a whole set of different column lengths. Knowing from the discussion of Figure 1 that the fastest way to generate a given number of plates is to find a column that yields this number if operated at the maximal pressure and that the kinetic plot curve connects all these maximal pressure-solutions, it should not be surprising to note from Figure 2(a) that, whatever efficiency would be needed, this efficiency can never be achieved faster than by a combination of flow-rate and column length lying on the enveloping kinetic plot curve. Similarly, it is impossible to find a better combination of column length and flow-rate giving you a higher efficiency in a given pre-set maximal time than for a combination lying on the kinetic plot envelope.

Fortunately, the criterion to get on the optimal enveloping curve is very simple: if you operate your column at the maximal pressure you're on the optimal envelope. Whereas, you are definitely operating under non-optimized conditions if you are using a column below the pressure limit.

Figure 6

In the latter case, you are wasting time because there is always a (larger) column length that would give you a better resolution in the same time — or bring you the same resolution, but in a shorter time. For example, if you normally use your columns around the optimal flow-rate, many of the available column lengths would bring you in a condition that is far remote from the kinetic plot curve (i.e, far remote from the optimal speed solution). In Figure 2, this can clearly be noted from the distance between the crosses and the kinetic plot curve (representing the optimal performance of the given particle type). These crosses mark the optimal flow-rate data point of each of the commercially available column lengths (including those accessible via column coupling).

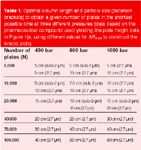
Table 1

The advantage of a maximal pressure operation versus an optimal flow-rate operation is illustrated in Figure 3. Supposing, for example, one would have a 600 bar instrument at one's disposal and supposing one would be using a 10 cm porous shell-column at its optimal flow-rate, one would be getting some 22000 theoretical plates in some 13 min (analysis time based on a component eluting at k= 10). The red vertical arrow in Figure 3 now shows that one could get the same resolution in only 5 min by switching to a 15 cm long column (this analysis time could even be reduced by an additional minute if a 17 cm long column would be available).

Getting a shorter analysis time by switching to a longer column may appear counterintuitive, but it follows from the fact that switching from the optimal flow-rate to a higher flow-rate (which inevitably includes an increase in column length if one is to reach the same efficiency) leads to shorter plate times [Figure 1(b)] and, therefore, to a shortening of the time needed to achieve a given plate count. This can also be understood from the fact that N basically is a function of both L and u, but more strongly depends on L than on u. Thus one can increase N at constant t₀ (deadtime) by increasing L and then increasing u to hold the t₀-time constant. The net effect is an increase in N/t₀. Clearly one can use this strategy to reduce t₀ while keeping N constant.

Figure 7

As a second example, operating a porous shell-column of 20 cm at the optimal flow-rate will give you 45 000 plates for a compound eluting at k = 10 in 26 min. Switching to a column length of 30 cm (vertical red arrow) and operating this column at the maximum pressure of 600 bar, will give the same amount of plates in only 12 min.

The above clearly illustrates that using an optimized column length can save a lot of analysis time. Obviously, this was already known from the early days of GC and HPLC.^1–4 but the present set of curves illustrates this in a very comprehensive yet clear way, using the results of a set of plate height measurements conducted with a pharmaceutical mixture.

Considering the other possible optimization route (i.e., keeping the same analysis time while trying to get the maximal efficiency or peak capacity) the red horizontal arrows that have been added to Figure 3 again show that if one would be using a 10 cm or a 20 cm porous shell column around its optimal flow-rate, one would again be much better off switching to a longer column. Starting from the 10 cm column, a switch to a 30 cm long column would yield a 2.1-fold increase in efficiency (while keeping the same analysis time), whereas, if one would be operating the 20 cm column around the optimum of the van Deemter curve, a switch to a 40 cm long column would yield a 1.7-fold increase in plate number, again without an increase in time.

Observations similar to those shown in Figures 2–3 can be made for 3.5 µm columns and for sub-2 µm columns. Figure 4 shows the kinetic plots obtained on a 15 cm column packed with 3.5 µm particles and rescaled to a series of different column lengths. Considering, for example, a 10 cm column operated at the optimal flow-rate, a plate count of 13000 can be obtained in 13 min. By switching to a column length of 20 cm (vertical red arrow), the same efficiency can be obtained in only 5 min if this longer column is operated at the maximum pressure. Keeping the analysis time constant (horizontal red arrow) a 2.2-fold increase in efficiency (going from 13000 plates to 28500 plates) can be obtained by switching to a 35 cm column. By using a more conventional column length of 30 cm, the efficiency can already be increased by a factor of 1.7 in only 10 min, given that this column is operated at the maximal pressure.

Whereas, the gain factors deduced from Figures 3–4 are merely predictions (albeit based on real experimental data), Figure 5 shows an example of how switching to a longer column and operating it at a larger pressure decreases the analysis time (and even increases the efficiency at the same time). In this example, switching from a 15 cm column operated at the optimal flow-rate to a 30 cm column operated at the maximal pressure (900 bar in the present case) allows an increase from 18000 plates in 13 min to 30000 plates in 8 min. Having had a column with an intermediate length (of 22 cm) at our disposal, the 18000 plates that can be obtained on the short column could have been obtained in some 5–6 minutes, instead of the current 13 min.

An optimization of the column length is also important in the case of sub-2 µm particles (Figure 6), although the potential gains in this case are slightly smaller than for the 2.7 and 3.5 µm particle cases considered in Figures 2–4. Using a 10 cm column packed with sub-2 µm particles, some 24000 plates can be obtained in 9 min when operating the column at the optimal flow-rate. Switching to a longer column (vertical red arrow) the same efficiency can be obtained on a 12 cm column but now in only 6 min. Furthermore, an increase in efficiency of a factor of 1.4 can be obtained in the same analysis time if a column of 15 cm is used (red horizontal arrow).

Figure 7 now combines the curves of Figures 3, 4 and 6, showing how a lab that has to solve a variety of difficult and easy separations would suffice having a 5 cm and a 10 cm column filled with sub-2 µm particles and a 5 cm, a 30 cm and a 60 cm coupled column system filled with porous shell particles in-house to be able to solve any of its separation problems in the minimal separation time (see dots). If desired, some intermediate lengths could be added to reduce the gap in between the optimal working points.

Obviously, changes in available pressure change the optimal column lengths and optimal particle sizes. This is illustrated in Table 1, giving the optimal particle size and column lengths yielding a given desired efficiency in the minimal analysis time (i.e., if operated at the maximal available pressure). This Table also shows that, the larger the available or allowable pressure, the longer the columns might become and the more precise the fine tuning of the column length can be done (the optimal column lengths range between 5–40 cm for 400 bar, whereas, they range from 5–70 cm for 1000 bar). This more precise fine tuning also indicates that the actual gain in analysis time one can make by switching to the optimal column length increases with increasing available pressure (data not shown here). Hence, adapting the column length more precisely to the exact efficiency needed becomes more rewarding if one has a high pressure instrument at one's disposal.

Conclusions

Although it might appear counterintuitive, using short columns does not always give you the fastest separation. Performing analysis around the optimal flow-rate of a column only gives you the shortest analysis time for that given plate count or peak capacity if that flow-rate corresponds to a pressure drop equalling the maximally available or allowable inlet pressure. If the optimal flow-rate raises a significantly lower pressure drop, there is always a longer column that gives the same efficiency in a shorter time (sometimes up to a factor of 2 or more). And there is also always an even longer column that gives a significantly larger efficiency (also up to a factor of two) in the same analysis time.

The introduction of very high pressure instruments, running up to 1000 bar instead of only up to 400 bar, has made the problem of column length optimization very timely again, because the gain one can realize by optimizing the column length increases with the available inlet pressure (at least for the current range of available particle sizes and column lengths).

The rather large gains in efficiency or speed of analysis that could be made if one could better tailor the column length shows how advantageous it would be if column and instrument manufacturers would devise solutions that allow for a more swift change in column length than is possible nowadays. This would allow to change the column length to one that is exactly long enough to produce the efficiency needed to solve the separation problem at hand while operating at the maximal pressure drop (i.e., at the optimal working point lying on the kinetic plot curve).

Acknowledgments

The authors thank Peter Schoenmakers for inspiring this article from one of his lectures. D. Ca. is supported through a specialization grant from the Instituut voor Wetenschap en Technologie (IWT) of the Flanders Region, Belgium.

Gert Desmet is a full professor in biochemical and chemical engineering at the vrije Universiteit Brussel, Brussels, Belgium. His research focuses on the miniaturization of separation methods and on the investigation of flow and mass transfer effects in chromatographic systems. Deirdre Cabooter has just entered her fourth year as a PhD student in the Department of Chemical Engineering of the Vrije Universitet Brussel (Belgium). Her research focuses on the use of kinetic plots to compare the performance limits of novel analytical instruments and columns. She has been the author and co-author of over 10 peer-reviewed papers.

References

1. J.H. Knox and M.J. Saleem, Chromatogr. Sci., 7, 614–622 (1969).

2. J.C. Giddings, Anal. Chem., 37, 60–63 (1965).

3. G. Guiochon, Anal. Chem., 53, 1318–1325 (1981).

4. H. Poppe, J. Chromatogr.A, 778, 3–21 (1997).

5. U.D. Neue and M. Kele, J. Chromatogr. A, 1149, 236–244 (2007).

6. G. Desmet, D. Clicq and P. Gzil, Anal. Chem., 77, 4058–4070 (2005).

7. G. Desmet et al., Anal Chem., 78, 2150–2162 (2006).

8. G. Desmet, LCGC Europe, 21(6), 310–315 (2008).