Approaches to Accelerate LC Method Development in the Laboratory Using Chemometrics and Machine Learning

Liquid chromatography (LC) is the single largest analytical field in terms of people involved and money spent. LC is crucial for almost all public and private sectors and the technique has seen tremendous technological advancements. Nevertheless, separations are often performed under suboptimal conditions and technological capabilities remain unused. Because expert knowledge and method development time are increasingly scarce, methods are often inefficient. Exploiting the full technological capabilities of liquid-phase separation technology requires deep knowledge and great time investments. Method optimization strategies that can simultaneously optimize the large number of parameters involved are therefore of great interest to chromatographers. This review examines different workflows that have been designed and used to facilitate and/or automate method development. In particular, focus is paid to the implementation of computer-aided workflows for the optimization of kinetic and thermodynamic parameters in LC, as well as on the possibilities to conduct this in a closed-loop fashion. Finally, the opportunities to use machine learning to achieve these goals is addressed.

Decades of research and development have allowed liquid chromatography (LC) to become the reliable and robust technique that we know today. This has paved the way for the development of increasingly advanced two-dimensional LC (2D-LC) methods with increased peak capacities, better use of mass spectrometry (MS), and new opportunities such as in-line reactions (1). For complex samples a 2D-LC method can be much faster than a one-dimensional (1D)-LC counterpart (2,3).

The development of 2D-LC has largely been driven by the growing interest of society and industry in understanding the increasingly complex and diverse samples, each with their own challenges associated.

The need to implement more powerful separation technologies is growing faster than the number of qualified users of multidimensional chromatography. The leading cause hampering further proliferation is the considerable amount of resources required for method development. This task is ever more daunting as method parameters are numerous and often interdependent, increasing the experience required to use all capabilities effectively.

This is illustrated in Figure 1, where the technological complexity (that is, the cost) is sketched against the information density (the benefit). There is a disproportionate increase in resources required to obtain further information. State-of-the-art separation technology such as 2D-LC can only make an impact if it can be efficiently employed.

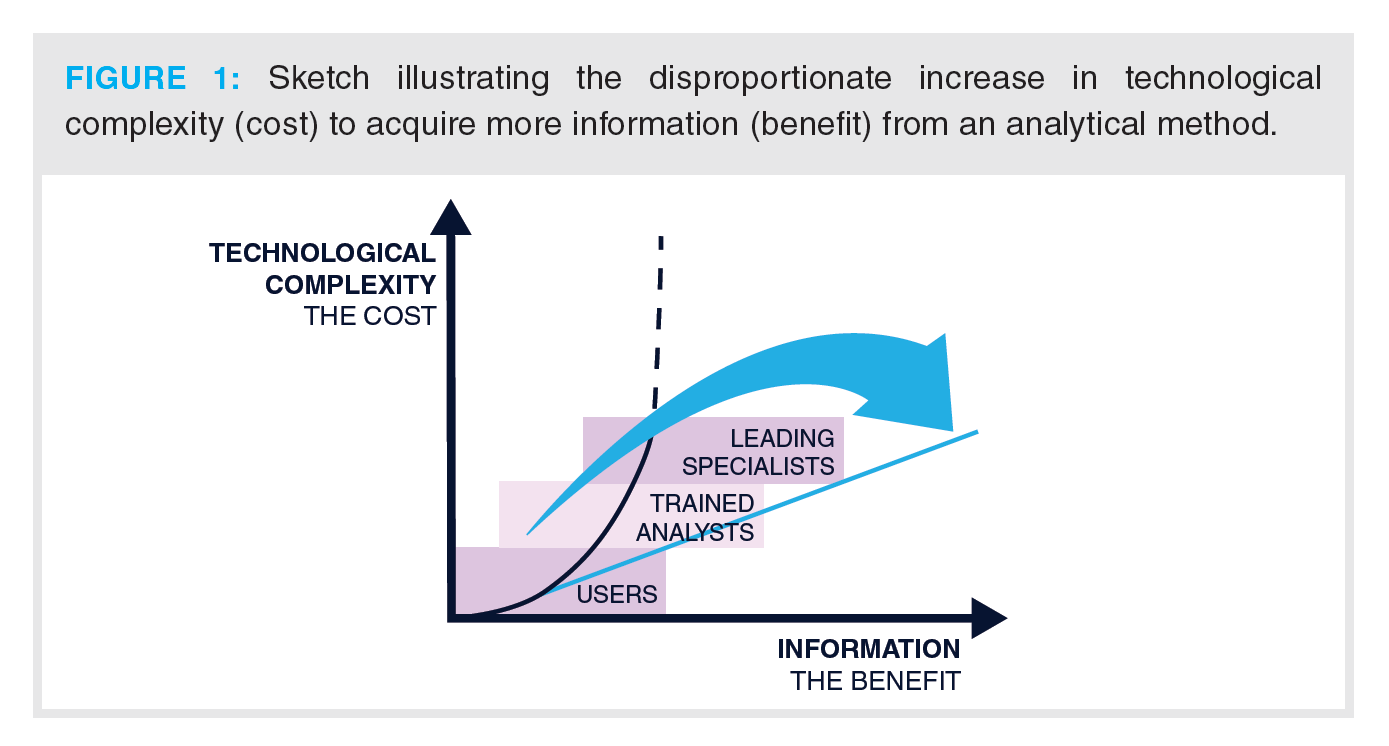
To facilitate this, researchers worldwide have been designing strategies with software to simplify method development (4–6) These and other method development and optimization strategies capitalize on theoretical understanding to simplify the method development process, as well as maximize its potential similar to the motto “work smarter, not just harder” (7). This review will map the method development process and identify categories of parameters that can be targeted. Different method optimization approaches that simplify or even automate sections of this workflow will then be examined. Finally, the opportunities to use machine learning to achieve in this context will be addressed.

Objectives of Chromatographic Method Development

Chromatographic method development is affected by the aim of the method. The optimization approaches for LC method development can be roughly classified as targeted and untargeted (8). Targeted approaches focus on specific analytes, whereas untargeted methods attempt to characterize the entire sample. This article will focus on untargeted methods, as targeted methods tend to have dedicated goals that cannot easily be generalized.

Generally, an analyst will start method development by using any information available on the sample chemistry, for example, Giddings’ sample dimensions (9), literature, and other resources to select an initial column (often a general-purpose column available in the laboratory) and generic method parameters (a generic linear gradient).

After the initial instrument parameters are established, the method can be evaluated based on its ability to provide the required critical information. When the method does not provide this information, method parameters can be adjusted to improve the method. This process is generally termed optimization. In chromatographic literature, the term optimization often represents divergent intentions based on the objective and the stage of the method development process. Indeed, “optimization” can refer to sample preparation (10), kinetic parameters that affect efficiency (11), the selection of a suitable stationary-phase chemistry (12), a reduction in analysis time (8), and so on. The common denominator in each case is that method parameters are adjusted with the aim of obtaining the desired information more effectively. Typically, this is evaluated through metrics that quantify the quality of separation, also known as quality descriptors.

To maximize the ability of a method to characterize a sample, untargeted approaches are often driven by such quality descriptors. For example, in the case where an analyst encounters a chromatogram saturated with peaks, maximization of the peak capacity (that is, the number of peaks that can be separated by the method) can be employed as a quality descriptor.

Untargeted optimization suffers from the vast number of adjustable parameters and the large interdependence between these. It is inherently difficult to predict whether a change in parameters will result in an improved method. Improving one metric (analysis time) may result in worsening another metric (resolution). Computer-aided development of a chromatographic method thus requires a balanced approach.

Resolution to Adjust a Chromatographic Method: One useful quality descriptor that quantifies the degree of separation, yet also instructs on possibilities to improve it, is the resolution (equation 1):

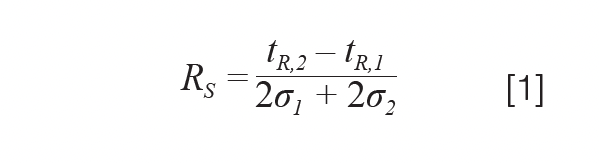
Here, the separation between analytes 1 and 2 is expressed with t_R and σ representing the retention time and peak standard deviation. When assuming that both analytes experience a similar column efficiency (that is, N₁ = N₂), we can re-write equation 1 as follows (13):

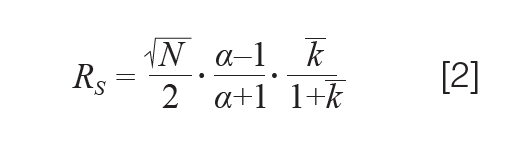
Now, we have resolution quantified as the product of three contributions: efficiency (N), selectivity (α), and average retention factor (k). Equation 2 demonstrates that the only means to adjust the separation is to change something within either of these three parameters.

At this point, it is important to acknowledge the significance of sample preparation and the crucial effect this has on the method development workflow. Sample preparation tends to be highly sample dependent, and it has been extensively treated elsewhere (14,15). It is outside the scope of this review.

Equation 2 can be schematically expressed in the context of method development workflows as depicted in Figure 2, which represents a typical case often faced by chromatographers. After having used their experience to select an appropriate column and initial method parameters, chromatographers are recommended to first adjust the method conditions by altering thermodynamic parameters that affect retention and selectivity. For example, they may change the gradient program or—if necessary—adjust the selectivity dramatically by selecting a different column or mobile-phase chemistry. Finally, they may opt to improve the efficiency or analysis time of the method by regarding the kinetic parameters. Different approaches that have been developed to facilitate method development through automated workflows or chemometrics will be reviewed in the following sections.

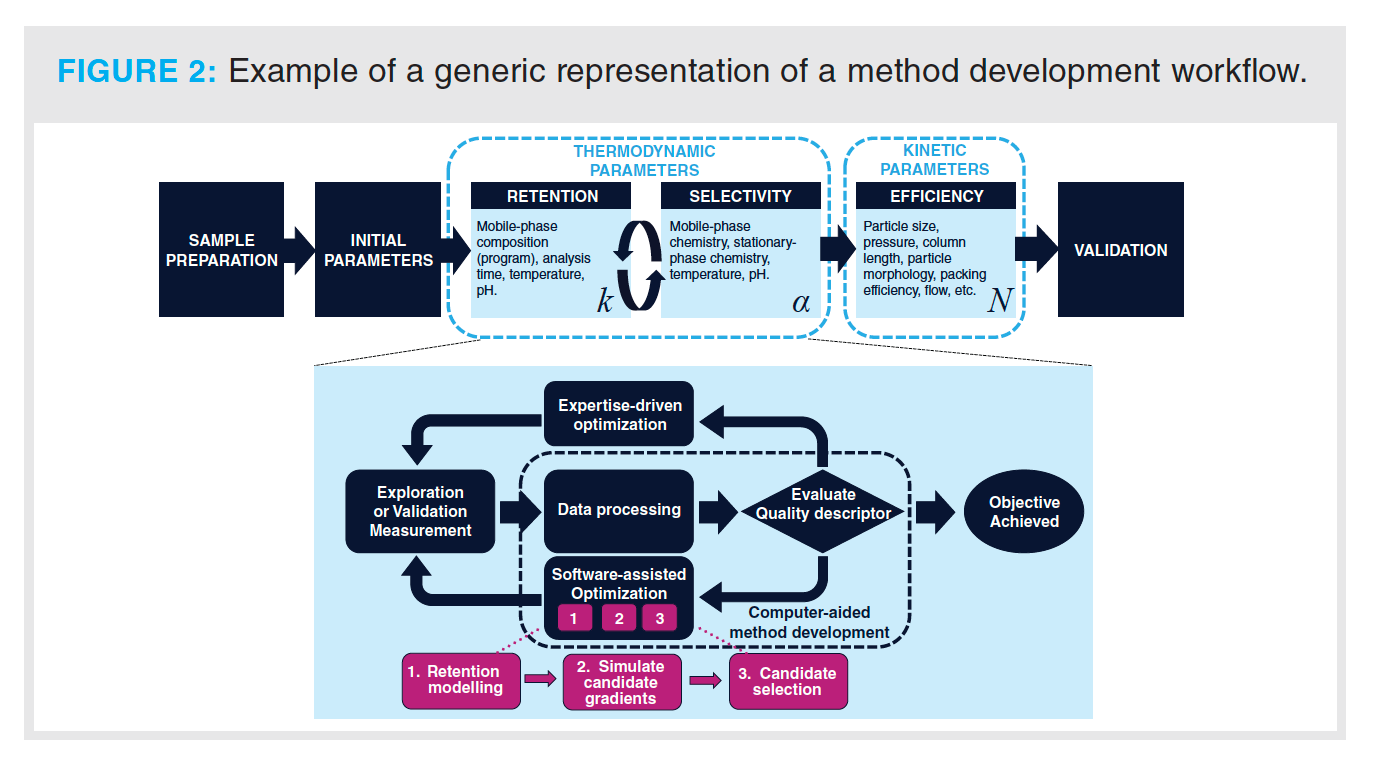
Kinetic Parameters

Improving the efficiency (that is, the theoretical plate number) of the separation provides a clear metric relevant to method optimization as it increases the peak capacity for the separation and decreases the likelihood of coelution. For 1D-LC it is possible to predict how different parameters will affect the efficiency. Another method is the use of kinetic plots (16). However, the square-root dependence of R_s on N implies a rapidly diminishing return on investment.

In comprehensive two-dimensional liquid chromatography (LC×LC) kinetic optimization schemes can be applied to substantially improve the method. This is attributed to the additional parameters, including the second-dimension (²D) column dimensions, and phenomena such as under-sampling (of the ¹D effluent) and ²D sample-dilution (17). Vivo-Truyols et al. proposed the use of sample-independent Pareto optimization (PO) for LC×LC (18). In this chemometric-driven approach, multiple method parameters (column dimension, flow rates, gradient slope) were varied and the effects thereof were evaluated using (theoretically related) quality descriptors such as peak capacity, analysis time, and dilution factor. The authors demonstrated that optimizing the kinetic parameters can be highly rewarding and that this approach is suited to deal with trade-offs between different objectives. The PO method provided optimal values for a large number of parameters, including ¹D and ²D particle sizes and column diameters, while taking into account pressure restrictions.

This work was extended by the group of de Villiers (11,19,20), who applied the PO strategy for the chromatographic separation of a phenolic red-wine extract (19), implemented a predictive kinetic-optimization tool for a hydrophilic interaction liquid chromatography×reversed-phase liquid chromatography (HILIC×reversed-phase LC) separation of procyanidins (11), and used the same tool to compare reversed-phase LC×HILIC and HILIC×reversed-phase LC for phenolic analysis (20). In all cases, optimization of kinetic parameters provided higher peak capacities and produced valuable knowledge on the influence of under-sampling, dilution factors, and band broadening.

Thermodynamic Parameters

Selectivity in liquid chromatography is influenced by the thermodynamic parameters related to analyte interactions with the mobile and stationary phases. Changes in mobile phase composition, gradient program, stationary phase chemistry, pH, or temperature can significantly affect the distribution of peaks in a chromatogram. While modifying the mobile phase, pH, or temperature is relatively straightforward in theory, in practice this may not suffice to meet the objectives of the separation. Changing the stationary phase in principle requires a re-optimization of the mobile phase, making it more expensive in terms of effort (apart from the column cost), but generally provides broader changes in selectivity.

Various strategies and workflows have been described to select appropriate chemistries for both the mobile and stationary phases in LC. One such strategy involves optimizing the parameters through a Design-of-Experiments (DoE) workflow, in which sets of parameters (for example, mobile phase, temperature, pH) are varied and an extensive screening is performed, often on multiple columns, to determine the optimum approach. Similar approaches are commonly used in the industry (21). They may be efficient in terms of manpower required, but can be quite inefficient in terms of numbers of measurements, time, solvents and instruments required.

For column selection, stationary phase characterization methods aim to simplify the end user’s choice of stationary phases based on characterizing the physicochemical interactions with small-molecule probes. For an extensive review the reader is referred elsewhere (22). The best-documented example is the hydrophobic subtraction model (HSM) developed by Snyder, Dolan, and co-workers, which may be used to select columns with different selectivity (23).

Recently, workflows have emerged related to selectivity screening for 2D-LC method development. For example, Zhang et al. developed a multiple heart-cut 2D-LC setup for pharmaceutical purity testing that enabled automated screening of the ²D selectivity (24). In other work, Wang et al. (25) used an automated column screening framework for analyzing chiral and achiral impurities, with online multiple heart-cutting 2D-LC; in a similar study, Zhang and co-workers described fast chiral and achiral profiling of compounds with multiple chiral centres by an LC–multicolumn-LC approach (26). Together with automated data acquisition, these workflows constituted a step forwards, but interpretation and processing of the data are still dependent on manual input and user experience.

Interpretive Automation

In an ideal scenario, a method development workflow must be capable of integrating all previously discussed parameters and optimizing these in an automated and interpretive manner. In this context, the word interpretive implies that the chromatograms are interpreted as a result of the elution of the individual analytes. In the workflow the peaks should be tracked and simple models may be established for each analyte—all of this in an unsupervised and automated manner. Based on the analyte models, many chromatograms can be simulated and the objective function can be optimized. Such a method development workflow has the potential to minimize manual input and the expertise required for developing complex methods.

Bos et al. developed the AutoLC approach, in which the mobile phase gradient was optimized in a closed-loop fashion (27). Based on an earlier theoretical LC×LC proof-of-principle study (28), and the pioneering work of Dolan and co-workers (29), Bos et al. designed an algorithm that could accommodate different chemometric optimization strategies. Two examples were presented: one using empirical retention modelling, and one using the machine-learning Bayesian optimization technique. In both cases, the algorithm developed multi-segment gradient programs to optimize the retention and selectivity of separations of a monoclonal antibody digest by LC–MS.

The examples above demonstrate the possibility of including computer-assisted optimization strategies for kinetic and thermodynamic parameters in automated workflows. However, despite the significant progress made, three major challenges remain that need to be addressed to achieve a closed-loop, interpretive algorithm for developing LC methods in a completely unsupervised and automated manner.

The first and arguably most important challenge is to define quality descriptors that can assess the quality of a separation. The success or failure of the optimization process critically depends on the objective function. The latter depends on quality descriptors that, in turn, may depend on chemical and physical parameters. The objective function serves as the primary driving force for every algorithm. Single-number descriptors, known as chromatographic response functions (CRFs), have been developed to quantify the critical information that the method is intended to provide. Various CRFs have been proposed in the past (30). Although many CRFs exist for 1D-LC, few are available for 2D-LC (31–36). Alvarez-Segura and co-workers recently included peak prominence in their CRF (33,34), Huygens et al. (35) introduced a CRF for 2D-LC based on peak purity, and Boelrijk et al. (36) presented a CRF based on connective components in graph theory to assess both separation quality and time. It has also been demonstrated that the selection of inappropriate quality descriptors can lead to suboptimal separations (27). Therefore, it is crucial to create CRFs that can effectively weigh quality descriptors, while the program provides quantitative information regarding various practical aspects of analytical queries, such as method time and sensitivity.

The second challenge is related to the data processing. The quality of the output of an algorithm relies strongly on the input data and the data processing. Any error in background correction, peak detection, or peak tracking can lead to cascading errors in later iterations (27). While MS provides information to reduce the errors in 1D-LC, data processing remains a significant challenge for LC×LC. This is especially the case for peak tracking, where an algorithm must establish the location of each analyte across multiple signals and account for incorrect clustering of coeluting peaks (37,38). In addition, it is difficult to quantitatively compare the performance of the large number of data processing approaches available (27,39).

The third challenge concerns the computation costs associated with the large number of simulations and the number of parameters that need to be optimized. Improving the performance of the algorithm either requires more measurements or more simulated data that resemble the experiments more closely. The former increases the amount of time and solvent needed, while the latter requires more computation power. Machine learning techniques may be employed to reduce the computation time required.

Machine Learning

Interest in machine learning methods is rapidly gaining momentum in the field of chromatography (7). The increasing computation power available, combined with the demand for advanced simulation tools, has led to the exploration of machine learning approaches for accelerated method development (40,41). Machine learning has the potential to enhance various stages of the chromatographic-analysis workflow, including baseline and noise correction (42), retention-time or retention-index prediction (43–45), peak detection (46,47), peak annotation (48), and classification (49). This section will focus on the utilization of machine learning to optimize the gradient program, which frequently relies on several of the aforementioned stages.

One type of machine learning is artificial neural networks (ANNs). The application of neural networks in chromatography has been explored in the past (50–53). In a recent study, Kensert et al. (42) investigated the potential use of reinforcement learning for selecting optimal isocratic scouting runs for retention modelling. The neural network was trained on simulated data using a Q-Learning algorithm and evaluated based on the accuracy of the retention predictions for 57 small-molecule analytes in situ experiments. While the work is promising, the algorithm from this study has only been tested on isocratic data for a specific reversed-phase LC setup with a limited number of simplistic molecules. A downside of the use of artificial neural networks is that they require a large amount of data for training. This can be mitigated with simulated data, but this carries a risk of the model not capturing the actual chromatographic space with sufficient accuracy (46).

Several authors have explored the potential of evolutionary algorithms to optimize gradient profiles (35,54). In particular, Hao et al. (54) used a genetic algorithm to optimize multi-linear gradient profiles for the separation of lignin-degradation products. They validated their simulations by comparison with experimental measurements and found good agreement. Huygens et al. (35) investigated evolutionary strategies for optimizing ¹D and ²D separations through in silico experiments of a LC×LC separation of 100 experiments. Their genetic algorithm required less than 100 experiments to reach a better CRF than a grid search of 625 experiments. This suggests that evolutionary algorithms have the potential to guide search-based method development, accelerate computational model-based method development, and deal with many parameters simultaneously. However, the authors simplified the experimental conditions by assuming perfect orthogonality, equal concentrations, and perfect Gaussian peaks. This raises concerns over the risk of oversimplification and the underutilization of the full range of variations in chromatographic conditions, as can also occur with neural networks.

One of the biggest limitations of applying machine learning is the required amount of data. An emerging optimization method that is less dependent on the amount of input data is Bayesian optimization, a type of machine learning tool that can optimize expensive-to-evaluate functions (expensive in terms of computation cost), even when there is a low amount of data available. Due to the compatibility with black box functions, only the score itself needs to be ascertainable, while the underlying mechanics or processes do not necessarily need to be understood or known. Boelrijk et al. investigated the potential use of Bayesian approaches for LC×LC in silico (36); they developed an unsupervised closed-loop algorithm to predict 1D-LC gradient profiles for a complex dyestuff mixture (55) and compared Bayesian optimization to retention modelling for automated method development (27). These studies demonstrated the versatility of Bayesian approaches and highlighted their applicability in method development workflows, with the added benefit of being less reliant on retention models and peak tracking. However, a potential limiting factor for LC×LC is the maximum number of parameters that can be optimized simultaneously. Due to the multivariate nature of the method, the number of necessary measurements for each additional parameter increases exponentially. The authors emphasized that the efficiency of Bayesian optimization is heavily dependent on the accurate definition of the objective function.

Machine learning approaches show tremendous potential to optimize the gradient program, yet the most advanced applications often have limitations that render them unsuitable for widespread use. This is partly due to the fact that these models can only handle scenarios that were present in the training data. Insufficient data can stem from a lack of appropriate standards or from insufficient resources to perform all the necessary measurements. One way to alleviate this issue is by employing simulated data, but this approach only works effectively if the simulated data closely resemble real-world situations, which is frequently not the case. With the rapid advancements in the field of machine learning, the issues currently encountered are expected to be addressed in the near future.

The Need for a Combined Effort

Driven by the ever-increasing need for more information, separation technology is advancing faster than our ability to use it to its full potential. Despite the enormous size and importance of the field, separations are often performed under suboptimal conditions and technical capabilities remain unused. For advancements in LC, such as 2D-LC, to make a significant impact, it is imperative that our community develops tools to fully exploit the current potential.

To this end, the chromatographic community must continue to deepen its understanding of fundamental concepts. This review has underlined the huge benefits and impressive advancements by scientists who have developed tools to streamline method development, focusing on kinetic or thermodynamic parameters—or both. Many of these advances are expressed as improved method development workflows that capture the experience and knowledge of the chromatographer.

However, the chromatographic community cannot do it alone. Indeed, we need the help of computers and information sciences. Automated LC method development workflows are rapidly advancing through the implementation of chemometric and machine learning algorithms. Nevertheless, despite the potential and promise of such algorithms to expedite method development, the challenges are still daunting and require a combined effort by the chromatographic and chemometric communities. Better ways must be found to mathematically express the chromatographic end goals, improve data analysis (peak detection), and invent smart algorithms that can interpret chromatographic data and combine these with fundamental kinetic (kinetic plots) and thermodynamic (retention models) concepts to create better methods. Meanwhile there is also the continuous need for chromatographers to deepen the understanding of physicochemical interactions of analytes inside our columns. The use of machine learning has recently been demonstrated by several groups to show great promise (35,55).

From the above-mentioned strategies it is clear that optimization workflows, especially for selectivity, remain heavily dependent on prior knowledge of the sample dimensionality or a trial-and-error approach. New machine learning algorithms should be able to optimize more parameters without needing unreasonable amounts of data. Other approaches may entail optimizing subsets of parameters at a time to lower the dimensionality of the problem or combining retention modelling with machine learning; in that way aspects that can be well described do not need to be captured in the machine learning models. The practical challenges are mostly on the required number of measurements or computations. Every optimization process is quicker when starting with a good setup. By scanning various columns at the start, a good estimate can be made of which columns show potential and are candidates for orthogonal separation in 2D-LC.

Computer-aided method development for LC has been under development for some four decades and it has failed to become common practice. However, with the rapid advances in LC, the gap between contemporary LC practice and potential has grown to a point where computer-aided method development is becoming a must. This need, in combination with the enormous growth in computation power and the dramatic advances in artificial intelligence, suggests that the time has come for computers to outperform analysts in LC method development.

Acknowledgements

This publication is part of the project Unleashing the Potential of Separation Technology to Achieve Innovation in Research and Society (UPSTAIRS) (with project number 19173) of the research programme TTW-VENI, which is financed by the Dutch Research Council (NWO).

References

1. Groeneveld, G.; Pirok, B. W. J.; Schoenmakers, P. J. Perspectives on the Future of Multi-Dimensional Platforms. Faraday Discuss. 2019, 218, 72–100. DOI: 10.1039/C8FD00233A
2. Stoll, D. R.; Wang, X.; Carr, P. W. Comparison of the Practical Resolving Power of One- and Two-Dimensional High-Performance Liquid Chromatography Analysis of Metabolomic Samples. Anal. Chem. 2008, 80 (1), 268–278. DOI: 0.1021/ac701676b
3. Uliyanchenko, E. Size-Exclusion Chromatography–From High-Performance to Ultra-Performance. Anal. Bioanal. Chem. 2014, 406 (25), 6087–6094. DOI: 10.1007/s00216-014-8041-z
4. Dolan, J. W.; Snyder, L. R.; Quarry, M. A. Computer Simulation as a Means of Developing an Optimized Reversed-Phase Gradient-Elution Separation. Chromatographia 1987, 24 (1), 261–276. DOI: 10.1007/BF02688488
5. Wang, L.; Zheng, J.; Gong, X.; Hartman, R.; Antonucci, V. Efficient HPLC Method Development Using Structure-Based Database Search, Physicochemical Prediction and Chromatographic Simulation. J. Pharm. Biomed. Anal. 2015, 104, 49–54. DOI:10.1016/j.jpba.2014.10.032
6. Hewitt, E. F.; Lukulay, P.; Galushko, S. Implementation of a Rapid and Automated High Performance Liquid Chromatography Method Development Strategy for Pharmaceutical Drug Candidates. J. Chromatogr. A 2006, 1107 (1–2), 79–87. DOI: 10.1016/j.chroma.2005.12.042
7. Stoll, D. The Future of Method Development for TwoDimensional Liquid Chromatography – Work Smarter, Not Just Harder? LCGC North Am. 2022, 40 (8), 379–382. DOI: 10.56530/lcgc.na.iy5385p1
8. Pirok, B. W. J.; Gargano, A. F. G.; Schoenmakers, P. J. Optimizing Separations in Online Comprehensive Two-Dimensional Liquid Chromatography. J. Sep. Sci. 2018, 41 (1), 68–98. DOI: 10.1002/jssc.201700863
9. Giddings, J. C. Sample Dimensionality: A Predictor of Order-Disorder in Component Peak Distribution in Multidimensional Separation. J. Chromatogr. A 1995, 703 (1–2), 3–15. DOI: 10.1016/0021-9673(95)00249-m
10. Liu, R.; Luo, Q.; Liu, Z.; Gong, L. J. Chromatogr. A 2020, 1629, 461473. DOI: 10.1016/j.chroma.2020.461473
11. Muller, M.; Tredoux, A. G. J.; de Villiers, A. Predictive Kinetic Optimisation of Hydrophilic Interaction Chromatography × Reversed Phase Liquid Chromatography Separations: Experimental Verification and Application to Phenolic Analysis. J. Chromatogr. A 2018, 1571, 107–120. DOI: 10.1016/j.chroma.2018.08.004
12. Lynen, F.; De Beer, M.; Hegade, R.; et al. Stationary-Phase Optimized Selectivity in Liquid Chromatography (SOS-LC) for Pharmaceutical Analysis. LCGC Eur. 2018, 31 (2), 82–89.
13. Foley, J. P. Resolution Equations for Column Chromatography. Analyst 1991, 116 (12), 1275–1279. DOI: 10.1039/AN9911601275
14. Hajeb, P.; Zhu, L.; Bossi, R.; Vorkamp, K. Sample Preparation Techniques for Suspect and Non-Target Screening of Emerging Contaminants. Chemosphere 2022, 287, 132306. DOI: 10.1016/j.chemosphere.2021.132306
15. Fu, Q.; Murray, C. I.; Karpov, O. A.; Van Eyk, J. E. Automated Proteomic Sample Preparation: The Key Component for High Throughput and Quantitative Mass Spectrometry Analysis. Mass Spectrom. Rev. 2023, 42 (2), 873–886. DOI: 10.1002/mas.21750
16. Desmet, G.; Clicq, D.; Gzil, P. Geometry-Independent Plate Height Representation Methods for the Direct Comparison of the Kinetic Performance of LC Supports with a Different Size or Morphology. Anal. Chem. 2005, 77 (13), 4058–4070. DOI: 10.1021/ac050160z
17. Stoll, D. R.; Carr, P. W. Eds., Multi-Dimensional Liquid Chromatography: Principles, Practice, and Applications; CRC Press, 2023.
18. Vivó-Truyols, G.; Van Der Wal, S.; Schoenmakers, P. J. Anal. Chem. 2010, 82 (20), 8525–853. DOI: 10.1021/ac101420f
19. Venter, P.; Muller, M.; Vestner, J.; et al., Comprehensive Three-Dimensional LC × LC × Ion Mobility Spectrometry Separation Combined with High-Resolution MS for the Analysis of Complex Samples. Anal. Chem. 2018, 90 (19), 11643–11650. DOI: 10.1021/acs.analchem.8b03234
20. Muller, M.; de Villiers, A. A Detailed Evaluation of the Advantages and Limitations of Online RP-LC×HILIC Compared to HILIC×RP-LC for Phenolic Analysis. J. Chromatogr. A 2023, 1692, 463843 (2023). DOI: 10.1016/j.chroma.2023.463843
21. Mattrey, F. T.; Makarov, A. A.; Regalado, E. L.; et al., Current Challenges and Future Prospects in Chromatographic Method Development for Pharmaceutical Research. TrAC Trends Analyt. Chem. 2017,95, 36–46. DOI: 10.1016/j.trac.2017.07.021
22. Žuvela, P.; Skoczylas, M.; Liu, J. J.; et al. Column Characterization and Selection Systems in Reversed-Phase High-Performance Liquid Chromatography. Chem. Rev. 2019, 119 (6), 3674–3729. DOI: 10.1021/acs.chemrev.8b00246
23. Snyder, L. R.: Dolan, J. W. The Hydrophobic-Subtraction Model for Reversed-Phase Liquid Chromatography: A Reprise. LCGC North Am. 2016, 34 (9), 730–741.
24. Zhang, K.; Li, Y.; Tsang, M.; Chetwyn, N. P. Analysis of Pharmaceutical Impurities Using Multi-Heartcutting 2D LC Coupled with UV-Charged Aerosol MS Detection. J. Sep. Sci. 2013, 36 (18), 2986–2992 (2013). DOI: 10.1002/jssc.201300493
25. Wang, H.; Herderschee, H. R.; Bennett, R.; et al. Introducing Online Multicolumn Two-Dimensional Liquid Chromatography Screening for Facile Selection of Stationary and Mobile Phase Conditions in Both Dimensions. J. Chromatogr. A 2020, 1622, 460895. DOI: 10.1016/j.chroma.2020.460895
26. Lin, J.; Tsang, C.; Lieu, R.; Zhang, K. Fast Chiral and Achiral Profiling of Compounds With Multiple Chiral Centers by a Versatile Two-Dimensional Multicolumn Liquid Chromatography (LC-mLC) Approach. J. Chromatogr. A 2020, 1620, 460987. DOI: 10.1016/j.chroma.2020.460987
27. Bos, T. S.; Boelrijk, J.; Molenaar, S. R. A.; et al. Chemometric Strategies for Fully Automated Interpretive Method Development in Liquid Chromatography. Anal. Chem. 2022, 94 (46), 16060–16068. DOI: 10.1021/acs.analchem.2c03160
28. Pirok, B. W. J.; Pous-Torres, S.; Ortiz-Bolsico, C.; Vivó-Truyols, G.; Schoenmakers, P. J. Program for the Interpretive Optimization of Two-Dimensional Resolution. J. Chromatogr. A 2016, 1450, 29–37. DOI: 10.1016/j.chroma.2016.04.061
29. Dolan, J. W.; Snyder, L. R.; Quarry, M. A. Computer Simulation as a Means of Developing an Optimized Reversed-Phase Gradient-Elution Separation. Chromatographia 1987, 24 (1), 261–276. DOI: 10.1007/BF02688488
30. Tyteca, E.; Desmet, G. A Universal Comparison Study of Chromatographic Response Functions. J. Chromatogr. A 2014, 1361, 178–190. DOI: 10.1016/j.chroma.2014.08.014
31. Duarte, R. M. B. O.; Matos, J. T. V.; Duarte, A. C. A New Chromatographic Response Function for Assessing the Separation Quality in Comprehensive Two-Dimensional Liquid Chromatography. J. Chromatogr. A 2012, 1225, 121–131. DOI: 10.1016/j.chroma.2011.12.082
32. Matos, J. T. V.; Duarte, R. M. B. O.; Duarte, A. C. Chromatographic Response Functions in 1D and 2D Chromatography as Tools for Assessing Chemical Complexity. TrAC Trends Analyt. Chem. 2013,45, 14–23. DOI: 10.1016/j.trac.2012.12.013
33. Alvarez-Segura, T.; Gómez-Díaz, A.; Ortiz-Bolsico, C.; Torres-Lapasió, J. R.; García-Alvarez-Coque, M. C. A Chromatographic Objective Function to Characterise Chromatograms with Unknown Compounds or Without Standards Available. J. Chromatogr. A 2015, 1409, 79–88. DOI: 10.1016/j.chroma.2015.07.022
34. Navarro-Huerta, J. A.; Alvarez-Segura, T.; Torres-Lapasió, J. R.; García-Alvarez-Coque, M. C. Study of the Performance of a Resolution Criterion to Characterise Complex Chromatograms with Unknowns or Without Standards. Anal. Methods 2017, 9 (29), 4293–4303. DOI: 10.1039/C7AY00399D
35. Huygens, B.; Efthymiadis, K.; Nowé, A.; Desmet, G. Application of Evolutionary Algorithms to Optimise One- and Two-Dimensional Gradient Chromatographic Separations. J. Chromatogr. A 2020, 1628, 461435. DOI: 10.1016/j.chroma.2020.461435
36. Boelrijk, J.; Pirok, B.; Ensing, B.; Forré, P. Bayesian Optimization of Comprehensive Two-Dimensional Liquid Chromatography Separations. J. Chromatogr. A 2021, 1659, 462628. DOI: 10.1016/j.chroma.2021.462628
37. Pirok, B. W. J.; Molenaar, S. R. A.; Roca, L. S.; Schoenmakers, P. J. Peak-Tracking Algorithm for Use in Automated Interpretive Method-Development Tools in Liquid Chromatography. Anal. Chem. 2018, 90 (23), 14011–14019. DOI: 10.1021/acs.analchem.8b03929
38. Molenaar, S. R. A.; Dahlseid, T. A.; Leme, G. M.; et al. Peak-Tracking Algorithm for Use in Comprehensive Two-Dimensional Liquid Chromatography – Application to Monoclonal-Antibody Peptides. J. Chromatogr. A 2021, 1639, 461922. DOI: 10.1016/j.chroma.2021.461922
39. Niezen, L. E.; Schoenmakers, P. J.; Pirok, B. W. J. Critical Comparison of Background Correction Algorithms Used in Chromatography. Anal. Chim. Acta 2022, 1201, 339605. DOI: 10.1016/j.aca.2022.339605
40. Houhou, R.; Bocklitz, T. Trends in Artificial Intelligence, Machine Learning, and Chemometrics Applied to Chemical Data. Anal. Sci. Adv. 2021, 2 (3–4), 128–141. DOI: 10.1002/ansa.202000162
41. Subraveti, S. G.; Li, Z.; Prasad, V.; Rajendran, A. Can a Computer “Learn” Nonlinear Chromatography?: Physics-Based Deep Neural Networks for Simulation and Optimization of Chromatographic Processes. J. Chromatogr. A 2022, 1672, 463037. DOI: 10.1016/j.chroma.2022.463037
42. Kensert, A. Collaerts, G.; Efthymiadis, K.; et al. Deep Convolutional Autoencoder for the Simultaneous Removal of Baseline Noise and Baseline Drift in Chromatograms. J. Chromatogr. A 2021, 1646, 462093. DOI: 10.1016/j.chroma.2021.462093
43. Albaugh, D. R.; Hall, L. M.; Hill, D. W.; et al. Prediction of HPLC Retention Index Using Artificial Neural Networks and IGroup E-State Indices. J. Chem. Inf. Model 2009, 49 (4), 788–799. DOI: 10.1021/ci9000162
44. Hall, L. M.; Hill, D. W.; Bugden, K.; et al. Development of a Reverse Phase HPLC Retention Index Model for Nontargeted Metabolomics Using Synthetic Compounds. J. Chem. Inf. Model 2018, 58 (3), 591–604. DOI: 10.1021/acs.jcim.7b00496
45. Ju, R.; Liu, X.; Zheng, F.; et al. Deep Neural Network Pretrained by Weighted Autoencoders and Transfer Learning for Retention Time Prediction of Small Molecules. Anal. Chem. 2021, 93 (47), 15651–15658. DOI: 10.1021/acs.analchem.1c03250
46. Kensert, A.; Bosten, E.; Collaerts, G.; et al. Convolutional Neural Network for Automated Peak Detection in Reversed-Phase Liquid Chromatography. J. Chromatogr. A 2022, 1672, 463005. DOI: 10.1016/j.chroma.2022.463005
47. Risum, A. B.; Bro, R. Using Deep Learning to Evaluate Peaks in Chromatographic Data. Talanta 2019, 204, 255–260. DOI: 10.1016/j.talanta.2019.05.053
48. Bonini, P.; Kind, T.; Tsugawa, H.; Barupal, D. K.; Fiehn, O. Retip: Retention Time Prediction for Compound Annotation in Untargeted Metabolomics. Anal. Chem. 2020, 92 (11), 7515–7522. DOI: 10.1021/acs.analchem.9b05765
49. Kantz, E. D.; Tiwari, S.; Watrous, J. D.; Cheng, S.; Jain, M. Deep Neural Networks for Classification of LC-MS Spectral Peaks. Anal. Chem. 2019, 91 (19), 12407–12413. DOI: 10.1021/acs.analchem.9b02983
50. Metting, H. J.; Coenegracht, P. M. J. Neural Networks in High-Performance Liquid Chromatography Optimization: Response Surface Modeling. J. Chromatogr. A 1996, 728 (1–2), 47–53. DOI: 10.1016/0021-9673(96)82447-2
51. Marengo, E.; Gianotti, V.; Angioi, S.; Gennaro, M. C. Optimization by Experimental Design and Artificial Neural Networks of the Ion-Interaction Reversed-Phase Liquid Chromatographic Separation of Twenty Cosmetic Preservatives. J. Chromatogr. A 2004, 1029 (1–2), 57–65. DOI: 10.1016/j.chroma.2003.12.044
52. Novotná, K.; Havliš, J.; Havel, J. Optimisation of High Performance Liquid Chromatography Separation of Neuroprotective Peptides: Fractional Experimental Designs Combined with Artificial Neural Networks. J. Chromatogr. A 2005, 1096 (1–2), 50–57. DOI:10.1016/j.chroma.2005.06.048
53. Malenović, A.; Jancic-Stojanovic, B.; Kostić, N.; Ivanović, D.; Medenica, M. Optimization of Artificial Neural Networks for Modeling of Atorvastatin and Its Impurities Retention in Micellar Liquid Chromatography. Chromatographia 2011, 73 (9–10), 993–998. DOI: 10.1007/s10337-011-1994-6
54. Hao, W.; Li, B.; Deng, Y.; et al. Computer Aided Optimization of Multilinear Gradient Elution in Liquid Chromatography. J. Chromatogr. A 2021, 1635, 461754. DOI:10.1016/j.chroma.2020.461754
55. Boelrijk, J.; Ensing, B.; Forré, P.; Pirok, B. W. J. Closed-Loop Automatic Gradient Design for Liquid Chromatography Using Bayesian Optimization. Anal. Chim. Acta 2023, 1242, 340789. DOI: DOI:10.1016/j.aca.2023.340789

Gerben B. van Henten is a PhD candidate at the Van ‘t Hoff Institute for Molecular Science (HIMS) at the University of Amsterdam.

Tijmen S. Bos is a postdoctoral researcher at the Van ‘t Hoff Institute for Molecular Sciences (HIMS) at the University of Amsterdam.

Bob W.J. Pirok is an assistant professor of analytical chemistry at the Van ‘t Hoff Institute for Molecular Science (HIMS) at the University of Amsterdam.